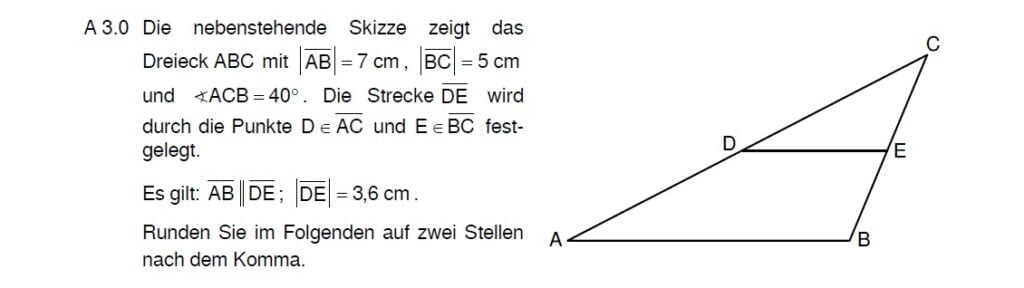

Lösung zu 3.1
Parallelität ist immer ein Hinweis auf den Vierstreckensatz.
\frac{|\overline{AB}|}{|\overline{DE}|} &= \frac{|\overline{BC}|}{|\overline{EC}|} \\
\frac{7}{3,6} &= \frac{5}{|\overline{EC}|} \\
7 \cdot |\overline{EC}| &= 5 \cdot 3,6 | :7 \\
|\overline{EC}| &= 2,57 \\
\\
|\overline{EB}| &= |\overline{BC}|- |\overline{EC}| \\
&= 5 – 2,57 = 2,43 cm \end{align} \)
Zurück zum MAP-Hack:

Lösung zu 3.2
Think outside the box… or the triangle. Setze dir einen zusätzlichen Punkt L, der senkrecht von E auf die Verlängerung auf AB steht.
\begin{align} &\angle BAC \text{ über den Sinussatz:} \\
\frac{\, |\overline{BC}| \,}{sin(\angle BAC)} &= \frac{\, |\overline{AB}| \,}{sin(\angle ACB)}\\
\frac{\, 5\, }{\, sin(\angle BAC) \,} &= \frac{\, 7 \,}{\, sin(40°) \,}\\
\Rightarrow sin(\angle BAC) &= 5 \cdot \frac{\, sin(40°) \,}{7} \\
\Rightarrow \angle BAC &= 27,33° \end{align}
Fälle zuerst das Lot von E auf AB. Der Lotfußpunkt P liegt dann außerhalb des Dreiecks. Im entstandenen Dreieck BLE kannst du die Höhe {latex]h = \overline{LE}[/latex] bestimmen. Dazu benötigst du den Winkel bei E, der ein Wechselwinkel zu CBA ist.
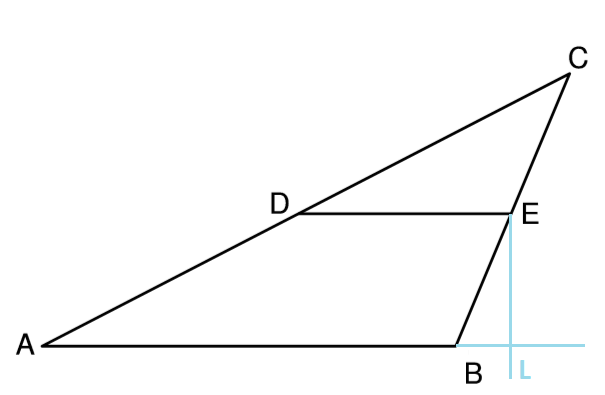
\begin{align} & \angle CBA \text{ mit der Innenwinkelsumme:} \\
\angle CBA &= 180° – 40° – 27,33 ° = 112,67° \\
\Rightarrow &112,67° – 90° = 22,67° \\
\angle CBE‘ &= \angle BEL \, (\text{Wechselwinkel}) \\
\\
&|\overline{LE}| = d \text{ mit dem Cosinus:} \\
cos(\angle BEL) &= \frac{|\overline{LE}|}{|\overline{EB}|} \\
cos (22,67°) &= \frac{d}{2,43} \, | \cdot 2,43 \\
\Rightarrow &d= 2,24 cm \end{align}

Du hast eine Frage zu einer Teilaufgabe oder zur Lösung? Schreib’ hier und du bekommst eine Antwort!