
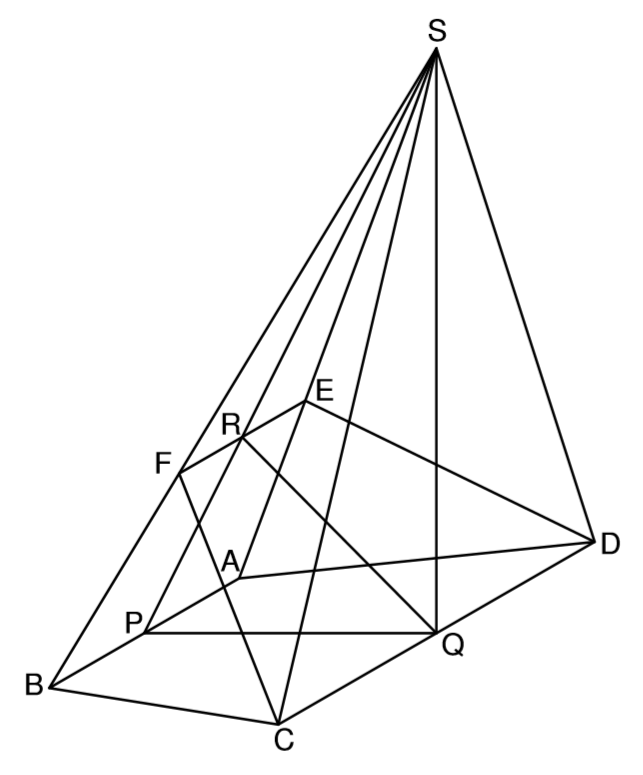

Lösung zu A2.1
\( \overline{PS}\) ist Teil eines rechtwinkligen Dreiecks.
\( \overline{EF}\) ist parallel zu \( \overline{AB}\), da kann man immer mal den Vierstreckensatz probieren.
\begin{align} &|\overline{PS}| \text{ mit dem Satz des Pythagoras:} \\
|\overline{PS}|^2 &= |\overline{PQ}|^2 + |\overline{QS}|^2 \\
|\overline{PS}| ^2 & = 4^2 + 8^2 \\
\Rightarrow &|\overline{PS}| = \sqrt{4^2 + 8^2} = 8,94 cm \\
\\
&|\overline{FE}| \text{ mit dem Vierstreckensatz:} \\
\dfrac{\, |\overline{PS}| \, }{|\overline{SR}|} &= \dfrac{\, |\overline{AB}| \,}{|\overline{FE}|} \\
&mit |\overline{SR}| = 8,94 – 3 = 5,94 \\
\dfrac{\, 8,94 \,}{5,94} &= \dfrac{6}{\, |\overline{FE}| \,} \\
\, 8,94 \cdot |\overline{FE}| &= 6 \cdot 5,94 \,\, |:8,94 \\
|\overline{FE}| &=3,99cm \end{align}
Alternativer Lösungsweg:
Zuerst bestimmst du den Winkel PSB im Dreieck SPB. Diesen Winkel kannst du im Dreieck RSF verwenden, um die Länge von [FR] zu bestimmen.
\begin{align} &\angle ABS \text{ mit dem Tangens:} \\
tan(\angle ABS) &= \frac{|\overline{BP}|}{|\overline{PS}|} \\
tan(\angle ABS) &= \frac{3}{8,94} \\
\Rightarrow & \angle ABS = 18,55° \\
\\
&x = 0,5\\
&\overline{FE} \text{ mit dem Tangens:} \\
tan(\angle ABS) &= \frac{x}{|\overline{SR}|} \\
tan(18,55°) &= \frac{x}{5,94} \, | \cdot 5,94 \\
x &= 1,99\\
& \Rightarrow |\overline{FE}| = 2x = 3,99 cm \end{align}
Zurück zum MAP-Hack:

Lösung zu 2.2
Dir fehlt noch die Höhe des Trapezes. Das ist nicht als Zwischenergebnis gegeben, aber anscheinend brauchst du QPS, um diese zu berechnen.
tan(\angle QPS) &= \frac{|\overline{SQ}|}{|\overline{PQ}|} \\
tan(\angle QPS) &= \frac{8}{4} \\
\Rightarrow &\angle QPS = 63,43°
\\
\\
&|\overline{RQ}| \text{mit dem Cosinussatz:} \\
|\overline{RQ}|^2 &= |\overline{PR}|^2 + |\overline{PQ}|^2 – 2 \cdot |\overline{RP}| \cdot |\overline{PQ}| \cdot cos(\angle QPS) \\
|\overline{RQ}|^2 &= 3^2 + 4^2 – 2 \cdot 3 \cdot 4 \cdot cos(63,43°) \\
\Rightarrow |\overline{RQ}| &= 3,78 cm \\
\\
&A \text{ mit der Flächenformel:} \\
A &= 0,5 \cdot (|\overline{CD}| + |\overline{FE}|) \cdot |\overline{RQ}| \\
&= 0,5 \cdot (10 + 3,99) \cdot 3,78 \\
\Rightarrow A& = 26,44 cm² \end{align} \)
Zurück zum MAP-Hack:

Lösung zu 2.3
Parallelitäten sind ein Hinweis auf den Vierstreckensatz. Steht das nicht schon weiter oben? =P
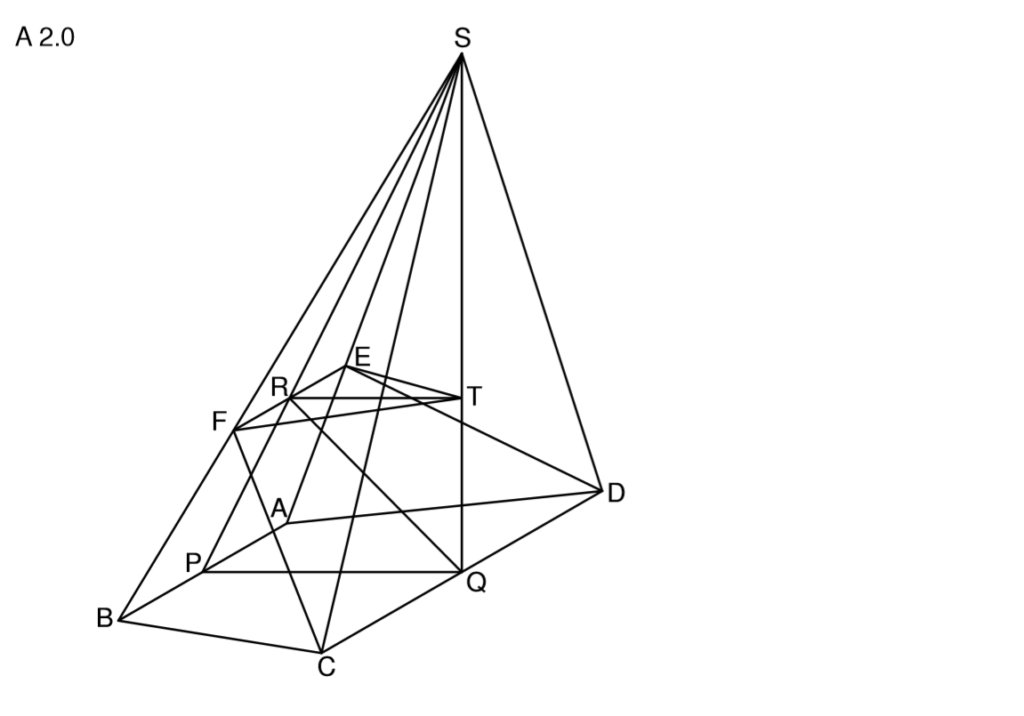
\( \begin{align} &|\overline{RT}| \text{ mit Vierstreckensatz:} \\
\frac{|\overline{PS}|}{|\overline{SR}|} &= \frac{|\overline{PQ}|}{|\overline{RT}|} \\
\frac{8,94}{5,94} & = \frac{4} {|\overline{RT}|} \\
\, 8,94 \, \cdot |\overline{RT}| &= 4 \cdot 5,94 |:8,94 \\
\Rightarrow &\overline{RT} = 2,66 cm \\
\\
& |\overline{RT}| \text{ mit Trigonometrie: (alternativer Weg)} \\
tan(\angle PSQ) &= \frac{|\overline{PQ}|}{|\overline{QS}|} \\
&= \frac{4}{8} \\
\Rightarrow &\angle PSQ = 26,57° \\
sin(\angle PSQ) &= \frac{|\overline{RT}|}{|\overline{SR}|}\\ sin(26,57°) &= \frac{|\overline{RT}|}{5,94} | \cdot 5,94 \\
\Rightarrow &|\overline{RT}| = 2,66 cm \\
\\
&|\overline{TS}| \text{ mit dem Satz des Pythagoras:} \\
|\overline{SR}|^2 &= |\overline{RT}|^2 + |\overline{ST}|^2 \\
5,94^2 &= 2,66^2 + |\overline{ST}|^2 |-2,66^2 \\
\Rightarrow |\overline{TS}| & = 5,31 cm \\
\\
&\text{Berechnung des Volumens:} \\
A_{\triangle EFT} & = \frac{1}{2} \cdot |\overline{EF}| \cdot |\overline{RT}| \\
&= \frac{1}{2} \cdot 3,99 \cdot 2,66 = 5,31 cm^2 \\
\\
V &= \frac{1}{3} \cdot 5,31 \cdot 5,31 = 9,40 cm^3 \end{align} \)

Ich habe bei Aufgabe 2.2 einen Fehler entdeckt bei Berechnung des Winkels QPS mit dem tan. haben sie statt QPS mit dem tan RQ mit dem tan geschrieben 🙂
Hallo Alex,
ich schaue mir 5 Minuten lang die Rechnung an und Frage mich „Was meint er denn?!“. Ja, in der Überschrift. Ouh man, das hätte ich nie gefunden. Danke!
meine Beschreibung war aber auch nicht die beste 😁
Du hast eine Frage zu einer Teilaufgabe oder zur Lösung? Schreib’ hier und du bekommst eine Antwort!