
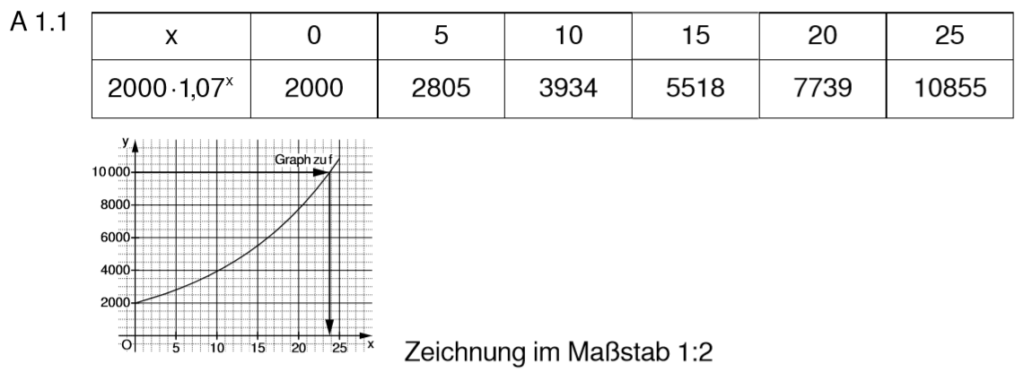
Lösung zu 1.1
Die Tabellen-Funktion des Taschenrechner hilft dir weiter. Achte auf die richtige Schrittweite!
Zurück zum MAP-Hack:

Lösung zu 1.2
Der Funktionsterm hat den Aufbau: f(x) = Startwert mal Wachstumsfaktor hoch x
Der Wachstumsfakto 1,07 ist um 0,07 größer als 1. Also nimmt der Wert jährlich um 7% zu.
Zurück zum MAP-Hack:

In der neuen Abschlussprüfung musst du diese Zeitspanne auch ausrechnen können. Probiere es aus, den Rechenweg findest du in der Lösung.
Lösung zu 1.3
Setze den Funktionsterm mit dem Zielwert gleich und löse die Gleichung.
Ablesen im KoSy
Das Fünffache von 2000 ist 10000. Gehe an der y-Achse zu 10000 und dann horizontal zum Graphen. Lies dort den x-Wert ab. Im Rahmen der Messgenauigkeit sind es 24 Jahre.
Rechenweg
\begin{align} y &= 2000 \cdot 1,07^x \text{ mit }y = 5 \cdot 2000 = 10000 \\
10000 &= 2000 \cdot 1,07^x \,\,\, |:2000 \\
5 &= 1,07^x \,\,\ |log_{1,07}\\
&\Rightarrow x = 23,79 \end{align}
Zurück zum MAP-Hack:

Lösung zu 1.4
x ist gegeben, y ist gesucht. Den Wert für x kannst du anhand des Datums ausrechnen.
\begin{align} &Berechnung \, der \, Dauer: \\ t &= 2065 – 2020 = 45 \\ \\ &Berechnung des Wertes: \\ f(45) &= 2000 \cdot 1,07^{45} \\ \Rightarrow y &= 42005 \end{align}
Die Aktien wären zu diesem Zeitpunkt 42005 € wert.
Zurück zum MAP-Hack:
Realitäts-Check der Aufgabe
Wie sinnvoll ist das eigentlich, was ihr da berechnen sollt? Im Video erkläre ich es euch!

Du hast eine Frage zu einer Teilaufgabe oder zur Lösung? Schreib’ hier und du bekommst eine Antwort!