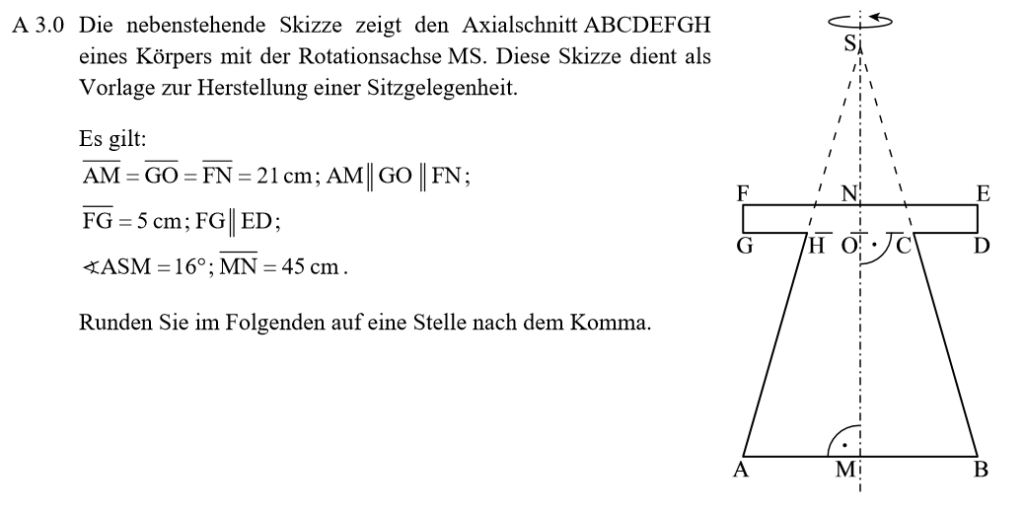
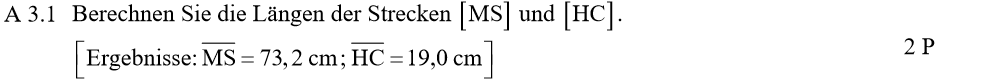
Lösung zu A3.1
AM||GO||FN : Parallelität ist immer ein Hinweis auf den Vierstreckensatz.
\begin{align} & |\overline{MS}| \, mit \, dem \, Tangens: \\
tan(\angle ASM) &= \frac{|\overline{AM}|}{|\overline{MS}|} \,\,\, |\cdot \overline{MS} : tan(\angle ASM) \\
|\overline{MS}|&= \frac{|\overline{AM}|}{tan(\angle ASM)} \\
&= \frac{21}{tan(16°)} \\
\Rightarrow &|\overline{MS}| = 73,2 cm \end{align}
DIe Länge der Strecke [HO]kann mit dem Vierstreckensatz berechnet werden. Dazu benötigst du die Länge der Strecke \(\overline{SO}\):
\begin{align} |\overline{SO}| &= |\overline{MS}| + |\overline{NO}| – |\overline{MN}| \\
&= 73,2 + 5 – 45 \\
\Rightarrow &|\overline{SO}| = 33,2 cm \\
\\
&|\overline{HO}| \, mit \, Vierstreckensatz: \\
\frac{|\overline{HO}|}{|\overline{AM}|} &= \frac{|\overline{SO}|}{|\overline{MS}|} \,\,\, | \cdot |\overline{AM}| \\
|\overline{HO}| &= \frac{|\overline{AM}| \cdot |\overline{SO}|}{|\overline{MS}|} \\
&= \frac{21 \cdot 33,2}{73,2} \\
\Rightarrow &|\overline{HO}| = 9,5 cm \\
\\
|\overline{HC}| &= 2 \cdot |\overline{HO}| \\
&= 2 \cdot 9,5 \\
\Rightarrow &|\overline{HC}| = 19,0 cm \end{align}
Zurück zum MAP-Hack:
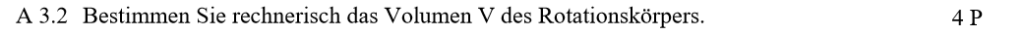
Lösung zu A3.2
Der Körper besteht aus einem Zylinder und einem Kegelstumpf. Achte auf die passenden Höhen!
Das gesuchte Volumen setzt sich aus den Volumina des Zylinders, des kleinen Kegels und des großen Kegels zusammen. Du berechnest diese Teilvolumina und setzt den gesuchten Körper zusammen.
\begin{align} V_{groß} &= \frac{1}{3} \cdot |\overline{AM}|^2 \cdot \pi \cdot |\overline{MS}| \\
&= \frac{1}{3} \cdot 21^2 \cdot \pi \cdot 73,2 \\
\Rightarrow &V_{groß} = 33804,8 cm^3 \\
\\
V_{klein} &= \frac{1}{3} \cdot |\overline{HO}|^2 \cdot \pi \cdot |\overline{SO}| \\
&= \frac{1}{3} \cdot (0,5 \cdot |\overline{HC}|) \cdot \pi \cdot (|\overline{MS}|- |\overline{MN}| + |\overline{FG}| ) \\
&= \frac{1}{3} \cdot (0,5 \cdot 19)^2 \cdot \pi \cdot (73,2 – 45 + 5) \\
\Rightarrow &V_{klein} = 3137,7 cm^3 \\
\\
V_{Zylinder}&= |\overline{GO}|^2 \cdot \pi \cdot |\overline{NO}| \\
&= 21^2 \cdot \pi \cdot 5 \\
\Rightarrow &V_{Zylinder} = 6927,2 cm^3 \\
\\
V &= V_{groß} – V_{klein} + V_{Zylinder} \\
&= 33804,8 – 3137,7 + 6927,2 \\
\Rightarrow &V = 37594,3 cm^3 \end{align}

Du hast eine Frage zu einer Teilaufgabe oder zur Lösung? Schreib‘ hier und du bekommst eine Antwort!