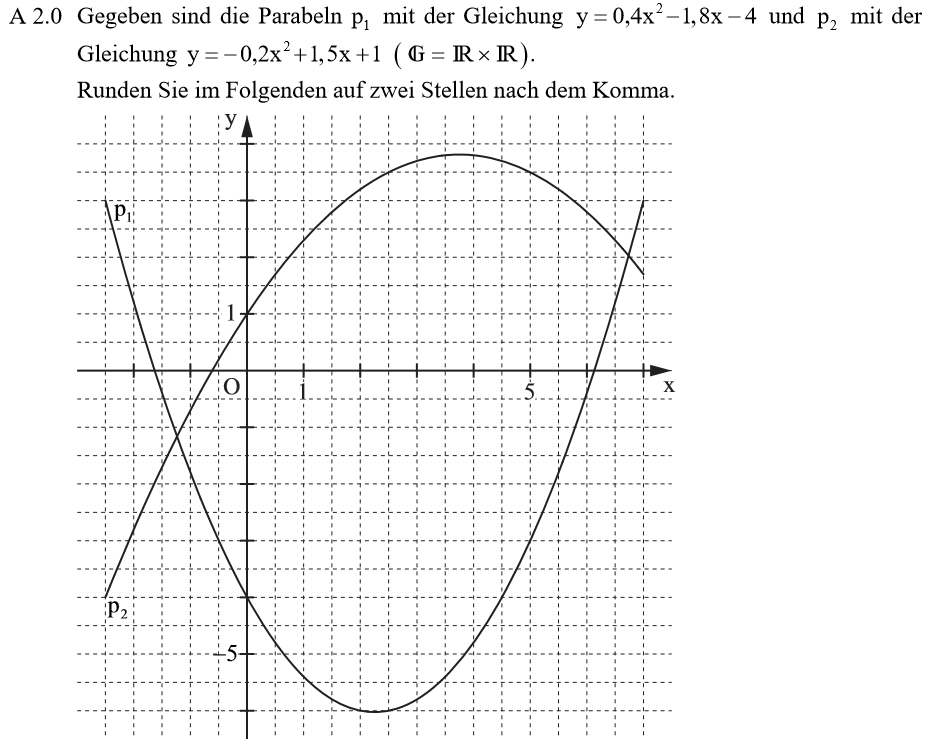

Lösung zu A2.1
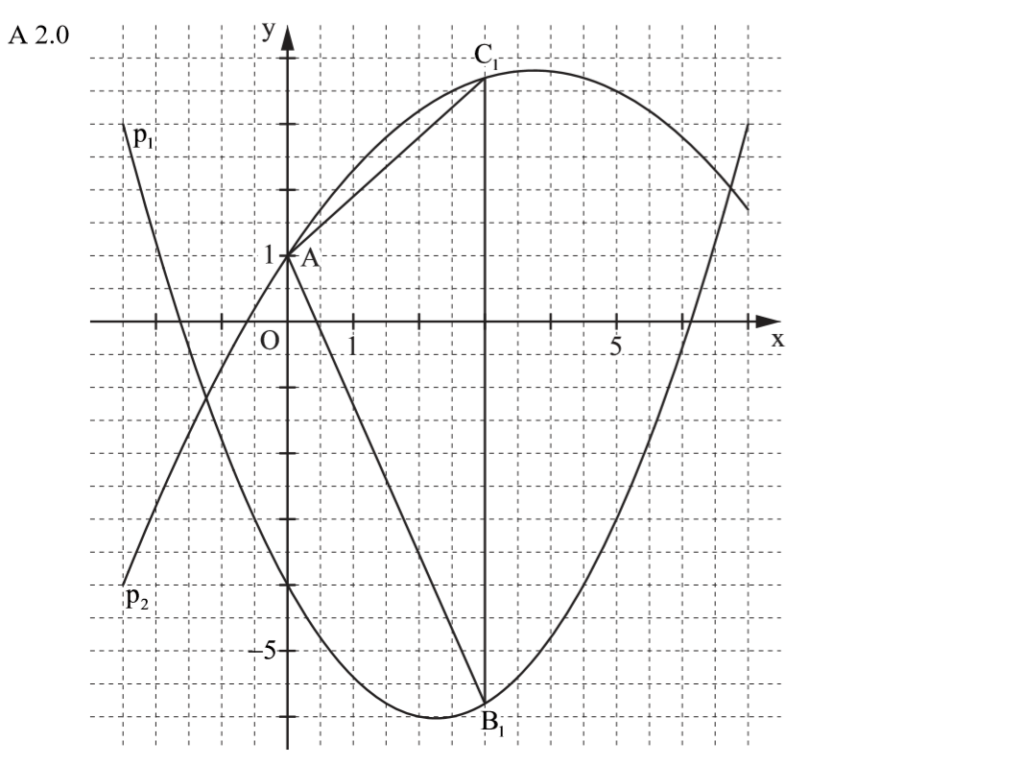
Die Punkte B und C haben die selbe Abszisse, also kannst du die Länge der Strecke [BC] durch „oben – unten“ berechnen.
\begin{align} & \overline{B_n C_n} (x) \, durch \, oben \, – \, unten: \\ \overline{B_n C_n} (x) &= y_{p_2} – y_{p_1} \\ &= -0,2x^2 + 1,5x + 1 – (0,4x^2 -1,8x – 4) \\ &= -0,2x^2 + 1,5x + 1 – 0,4x^2 +1,8x + 4 \\ \Rightarrow & \overline{B_n C_n} (x) = (-0,6x^2 + 3,3x + 5) LE \end{align}
Zurück zum MAP-Hack:

Lösung zu A2.2
Nimm den funktionalen Zusammenhang für die Länge der Strecke [BC] und setzte sie gleich 10. Löse anschließend die quadratische Gleichung.
\begin{align} \overline{B_n C_n} &= 10 \\ -0,6x^2 + 3,3x + 5 &= 10 \, \, \, |-10 \\ -0,6x^2 + 3,3x -5 &= 0 \\ \Rightarrow GTR: \, Keine \, Lösung \end{align}
Weil die Gleichung keine Lösung hat, gibt es kein Dreickeck mit der Seitenlänge 10 von [BC].
Es ist auch möglich den Extemwert des quadratischen Terms mit dem GTR zu bestimmen: Maximaler Termwert: 9,54 LE. Weil die maximale Strecke 9,54 LE lang ist, gibt es keine Seite mit Länge 10 LE.
Zurück zum MAP-Hack:

Lösung zu A2.3
Nach dem Mittelpunk wird selten gefragt! Kann man lernen, aber erst, wenn die Grundlagen sitzen!
Der Mittelpunkt ergibt sich durch Mittlung der y-Koordinaten. Sie werden addiert und durch zwei geteilt. Genau wie beim Klassendurchschnitt bei zwei Schülern.
\begin{align} y_M &=\frac{y_B + y_C}{2} \\ &= \frac{-0,2x^2 + 1,5x + 1 + 0,4x^2 – 1,8x – 4} {2} \\ &= \frac{0,2x^2 – 0,3x – 3}{2} \\ \Rightarrow &y_M = 0,1x^2 -0,15x -1,5 \end{align}

Lösung zu A2.4
Strategie-Tipp vorneweg: Weil die funktionale y-Koordinate des Mittelpunkts in der vorletzten Aufgabe berechnet wurde, wirst du ihn jetzt brauchen.
Das Dreieck soll gleichschenklig mit [BC] als Basis sein. Ein gleichschenkliges Dreieck ist achsensymmetrisch und die Achse steht senkrecht auf die Basis und läuft durch den gegenüberliegenden Punkt. Weil die Basis [BC] vartikal verläuft, muss die Symmetrieachse horizontal verlaufen. A und der Mittelpunkt M müssen also die selbe y-Koordinate haben, weil die Verbindungslinie (Symmetrieachse) sonst nicht horizontal verläuft.
\begin{align} y_M &= y_A \, mit \, y_A = 1 \\ y_M &= 1 \\ 0,1x^2 – 0,15x – 1,5 &= 1 \,\, \, |-1 \\ 0,1x^2 -0,15x -2,5 &= 0 \\ \Rightarrow >R: (x_1 = -4,31 \lor) x_2 = 5,81 \end{align}

bei der Lösung zu A 2.3 ist im 3 Schritt -0.2x^2 statt 0.2x^2
Danke! Ist ausgebessert.
Hallo eine Frage, ist es möglich bei der 2.2 auch einfach die maximale Länge von BC zu bestimmen und es damit zu begründen.
Hallo Korbinian,
ja, das funktioniert auch. Bei diesem Typ von Aufgaben gibt es immer diese beiden Lösungsmglichkeiten.
Du hast eine Frage zu einer Teilaufgabe oder zur Lösung? Schreib‘ hier und du bekommst eine Antwort!