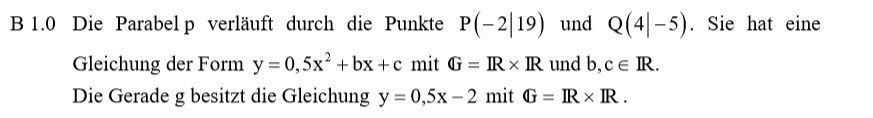

Lösung zu B1.1
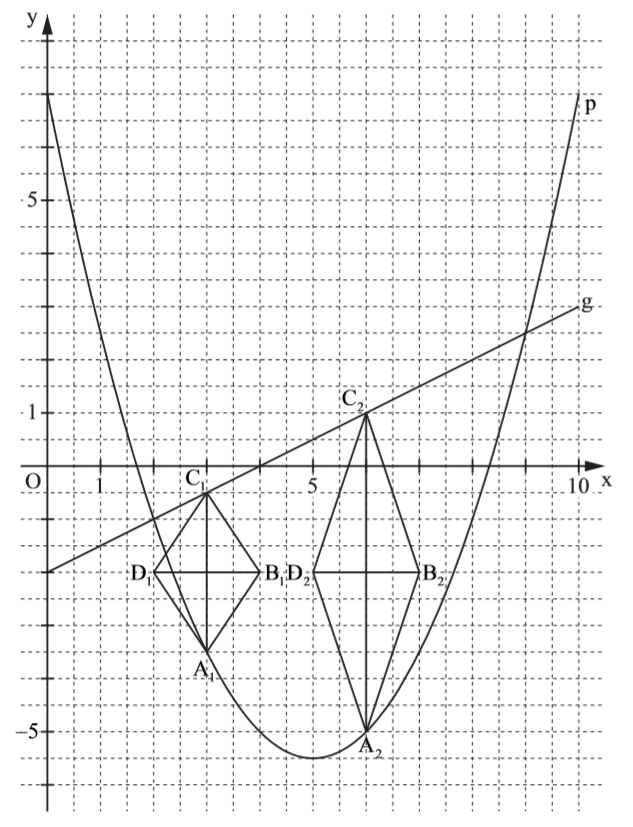
Setze die Punkte P(-2|19) und Q(4|-5) jeweils in die Parabelgleichung \( y = 0,5 x^2 + bx + c \) ein, um ein Gleichungssystem aufzustellen. Löse es dann mit dem GTR
\( \begin{align} (I) y &= 0,5 x^2 + bx + c \\ & \land \, \, \, (II) y = 0,5 x^2 + bx + c \\ (I) 19 &= 0,5 \cdot (-2)^2 + b \cdot (-2) + c \\ & \land \, \, \, (II) -5 = 0,5 \cdot 4^2 + b \cdot 4 + c \\ Umformen \, &zu \, “= 0”: \\ (I) -2b + c – 17 &= 0 \\ & \land \, \, \, (II) 4b + c + 13 = 0 \\ \Rightarrow GTR: \, b &= -5 \, \land \, c = 7 \end{align} \)Zurück zum MAP-Hack:

Lösung zu B1.2
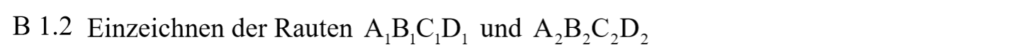
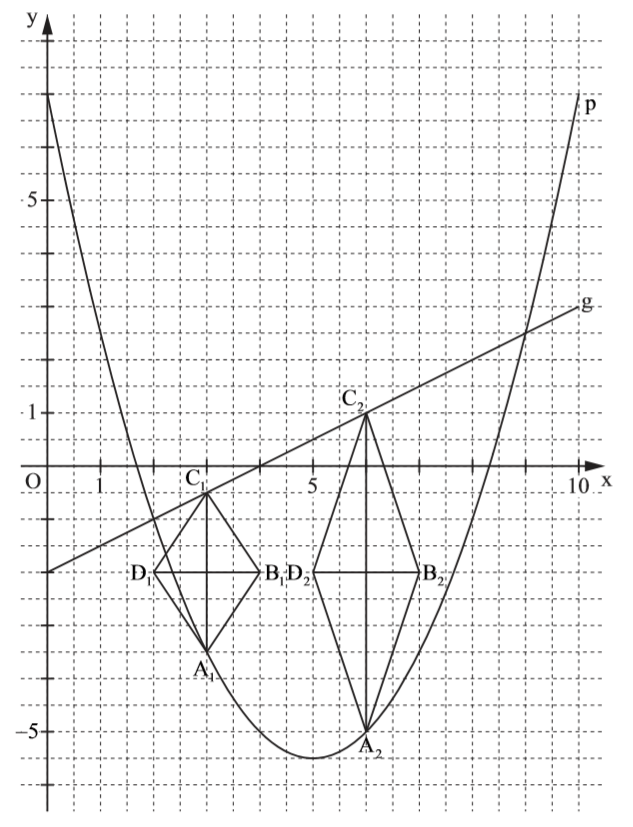
Zurück zum MAP-Hack:

Lösung zu B1.3
Berechne die Schnittpunkte von g und p. Setze dazu die Funktionsterme gleich und löse nach „= 0“ auf und löse die quadratische Gleichung mit dem GTR.
\( \begin{align} y_{Parabel} &= y_{Gerade} \\ 0,5x^2 -5x + 7 &= 0,5x – 2 \, \, \, | \, – 0,5x + 2 \\ 0,5x^2 -5,5x + 9 &= 0 \\ \Rightarrow GTR: \, x_1 = 2 \lor x_2 = 9 \\ \Rightarrow &x \in ]2; 9[ \end{align} \)Zurück zum MAP-Hack:

Lösung zu B1.4
Berechnung von \( \overline{A_nC_n} \) durch „oben – unten“:
\( \begin{align} \overline{A_n C_n} &= 0,5x – 2 – (0,5x^2 – 5x +7) \\&= 0,5x – 2 – 0,5x^2 +5x – 7 \\
\Rightarrow & \overline{A_n C_n} = (-0,5x^2 + 5,5x -9) LE \\
\\
&Berechnung \, von \, \overline{A_2C_2}: \\
\overline{A_2C_2} & = (-0,5 \cdot 6^2 + 5,5 \cdot 6 – 9 ) = 6 LE \\
\\
&Berechnung \, von \, \varphi : \\
tan (\frac{\varphi}{2}) &= \frac{0,5 \cdot \overline{B_2 D_2}}{0,5 \cdot \overline{A_2 C_2}} \\ tan (\frac{\varphi}{2}) &= \frac{0,5 \cdot 2}{2 \cdot 6} \\
\Rightarrow \frac{\varphi}{2} &= 18,435° \\
\varphi &= 36,87° \\
\\
&Berechnung \, von \, \overline{A_2 B_2}: \\
\overline{A_2 B_2}^2 &= (0,5 \cdot \overline{B_2 D_2})^2 + (0,5 \cdot \overline{A_2 C_2})^2 \\
\overline{A_2 B_2}^2 &= (0,5 \cdot 2)^2 + (0,5 \cdot 6)^2 \\
\Rightarrow &\overline{A_2 B_2} = 3,16 LE \end{align} \)
Zurück zum MAP-Hack:
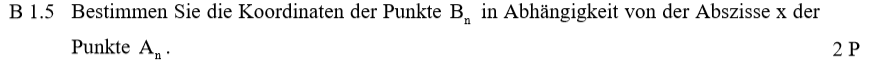
Lösung zu B1.5
Um die Punkte \( B_n \) zu finden, musst du eine LE rechts vom Mittelpunkt der Diagonalen [AC] suchen. Weil die Abszisse gleich ist, ist die x-Koordinate des Mittelpunktes x. Die y-Koordinate erhältst du durch die Formel für den Mittelpunkt:
\( \begin{align} y_{Mittelpunkt} &= \frac{oben + unten}{2} = \frac{0,5x^2 – 4,5x + 5}{2} \\ & = 0,25x^2 – 2,25x + 2,5 \\ \Rightarrow &B_n (x+1|0,25x^2 – 2,25 x + 2,5) \end{align} \)
Lösung zu B1.6
Der größte Flächeninhalt ist 6,13 FE und damit kleiner als 7 FE.

Hallo, ich habe eine Frage zur 1.5…warum kann man nicht einfach sagen, die y-Koordinate von B in Abhängigkeit von x ist immer die Hälfte der Strecke AnCn?
Die Idee ist gut, aber die Hälfte der Länge der Strecke sagt ja nichts über die Lage im Koordinatensystem aus. Eine Strecke der Länge 5 hat ja nichts mit der Koordinate 5 zu tun.
Hallo Robin,
das klingt nach einem Connection-Problem. Einfach die Seite noch laden, die Inhalte sind alle online.
Hallo ich hab eine frage zur AP 2018 haupttermin bei nummer 1.6
Warum muss ich
AnCn*BnCn rechen.
Warum kann ich nicht von AnCn die max. Länge ausrechnen und die Dan dafür einsetzten.?
Hallo Vroni,
schön, dass du fragst! Du kannst auch die maximale Länge von AnCn ausrechnen, denn BnDn ist ja konstant. Dein Gedanken ist völlig richtig. Als Korrektor würde ich dann aber einen Satz Erklärung verlangen, denn es ist ja nach dem Flächeninhalt der Rauten gefragt und nicht nach der Streckenlänge. Zum Beispiel „Weil BnDn konstant ist, ist der Flächeninhalt der Rauten maximal, wenn die Strecke AnCn maximal ist … *Rechnung*“.
Frag‘ gerne wieder!
Tb.Cb
Du hast eine Frage zu einer Teilaufgabe oder zur Lösung? Schreib‘ hier und du bekommst eine Antwort!