Lösung zu A3.1
Lösung als Text
Lösung als Video
\( \begin{align} &Berechnung \, von \, \overline{MD}: \\ tan(\angle SDM) &= \frac{\overline{MS}}{\overline{MD}} \, \, | \cdot \overline{MD} : tan(\angle SDM) \\ &= \frac{5}{tan(71,6°)} \\ \Rightarrow & \overline{MD} = 1,7 cm \\ \\&Berechnung \, von \, \overline{AN}: \\ tan(\angle SAN) &= \frac{\overline{NS}}{\overline{AN}} \, \, | \cdot \overline{AN} |: tan(\angle SAN) \\ \overline{AN} &= \frac{\overline{NS}} {tan(\angle SAN)} \, mit \, \angle SAN = 71,6° \, \\ &= \frac{3}{tan(71,6°)} \\ \Rightarrow & \overline{AN} = 1,0 cm \end{align} \)
Ansatz über Vierstrecken auch möglich!
\( \begin{align} \frac {\overline{AN}}{\overline{MD}} &= \frac{\overline{NS}}{\overline{MS}} \\ & … \end{align}\)Zurück zum MAP-Hack:
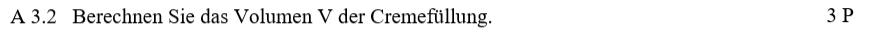
Lösung zu A3.2
Lösung als Text
Lösung als Video
Achtung, diese Aufgabe stellt dir eine Falle. Das Volumen der Cremefüllung bekommst du, indem du vom Gesamtvolumen (100%) den Schokoladenanteil (89%) abziehst. 89% sind Schokolade, bleiben 11% für die Cremefüllung. Berechne zuerst das Gesamtvolumen und dann 11% davon.
\( \begin{align} &Berechunng \, des \, Gesamtvolumens: \\ V_{Gesamt} & = V_{groß} – V_{klein} \\ &= \frac{1}{3} \cdot \overline{MD}^2 \cdot \pi \cdot \overline{MS} – \frac{1}{3} \cdot \overline{AN}^2 \cdot \pi \cdot \overline{NS} \\ &= \frac{1}{3} \cdot 1,7^2 \cdot \pi \cdot 5 – \frac{1}{3} \cdot 1^2 \cdot \pi \cdot 3 \\ \Rightarrow &V_{Gesamt} = 12,0 cm^3 \\ \\ &Berechnung \, der \, Cremefüllung: \\ \ V_{Creme} &= 11 \% \cdot 12,0 cm^3 = 1,3 cm^3 \end{align} \)
Du hast eine Frage zu einer Teilaufgabe oder zur Lösung? Schreib’ hier und du bekommst eine Antwort!