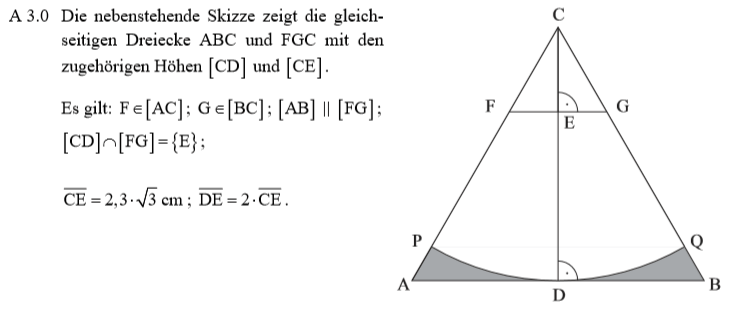

Lösung zu A3.1
Zuerst berechnest du die Länge der Strecke [CD], um dann im halben Dreieck den Satz des Pythagoras zu verwenden:
\begin{align} &\overline{CD} \, durch \, Addition: \\ \overline{CD} &= \overline{CE} + \overline{DE} \\ &= \overline{CE} + 2 \cdot \overline{CE} \\ &= 2,3 \cdot \sqrt{3} + 2 \cdot 2,3 \cdot \sqrt{3} \\ \Rightarrow &\overline{CD} = 6,9 \cdot \sqrt{3} \\ \\ &a \, mit \, dem \, Satz \, des \, Pythagoras: \\ \overline{AC}^2 &= \overline{AD}^2 + \overline{CD}^2 \\ a^2 &= (0,5a)^2 + (6,9 \cdot \sqrt{3})^2 \,\,\, |-(0,5a)^2 \\ 0,75a^2 &= (6,9 \cdot \sqrt{3}^2 \,\,\, | : 0,75 \\ a^2 &= (6,9 \cdot \sqrt{3})^2 : 0,75 \\ \Rightarrow &a = 13,8 cm \end{align}
Zurück zum MAP-Hack:

Lösung zu A3.2
Der gesuchte Flächeninhalt ergibt sich, indem man vom Flächeninhalt des Dreiecks ABC den Flächeninhalt des Kreissektors abzieht.
\begin{align} A_{ABC} &= 0,5 \cdot g \cdot h \\
&= 0,5 \cdot 13,8 \cdot 6,9 \cdot \sqrt{3} \\
\Rightarrow &A_{ABC} = 82,46 cm^2 \\
\\
A_{Sektor} &= \frac{60°}{360°} \cdot a \cdot \pi \\
&= \frac{1}{6} \cdot (6,9 \cdot \sqrt{3})^2 \cdot \pi \\
\Rightarrow &A_{Sektor} = 74,79 cm^2 \\
\\
A &= A_{ABC} – A_{Sektor} \\ &= 82,46cm^2 – 74,79 cm^2 \\ \Rightarrow A&= 7,67 cm^2 \\
\\
&p \, mit \, der \, Formel: \\ p &= \frac{A}{A_{ABC}} \cdot 100 \% \\ &= \frac{7,67}{82,46} \cdot 100 \% \\
\Rightarrow &p = 9,30\% \end{align}
