

Lösung zu B1.1
Der Scheitelpunkt der Parabel ist gegeben, also arbeitest du mit der Scheitelform. Setze den Öffnungsfaktor 0,5, den du aus der Angabe weißt, in die Scheitelform \( y = a \cdot (x – x_s)^2 + y_s \) ein. Danach setzt du die Koordinaten von S(0,5|1) ein. Löse die Klammer mit einer binomischen Formel auf und vereinfache soweit wie möglich.
Der Scheitelpunkt der Parabel ist gegeben, also arbeitest du mit der Scheitelform. Setze den Öffnungsfaktor 0.5, den du aus der Angabe weißt, in die Scheitelform \(y = a \cdot (x – x_s)^2 + y_s \) ein. Danach setzt du die Koordinaten von \(S = (0,5|1)\) ein. Löse die Klammer mit einer binomischen Formel auf und vereinfache soweit wie möglich:
\begin{align} y &=\, \tfrac 12 \cdot (x – 0.5)^2 + 1 \\
&=\, \tfrac 12 \cdot \left(x^2 – 2\cdot0.5\cdot x + 0.25\right) + 1 \\
&=\, \tfrac 12 \cdot x^2 – 0.5\cdot x + 1.125 \end{align}
Also ist \(b = -0,5\) und \(c = 1,125\).
Zurück zum MAP-Hack:
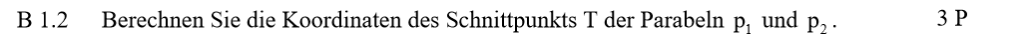
Lösung zu B1.2
Der Schnittpunkt \( P = (x_P|y_P)\) wird berechnet, indem im ersten Schritt die Gleichungen gleichgesetzt werden und \( x_P\) ermittelt wird.
Natürlich kannst du einfach „= 0“ auflösen und mit dem GTR lösen, aber hier gibt es mal die schriftliche Lösung.
\begin{align} y_P &=\, p_1(x_P) = \tfrac 12 \cdot x_P^2 – 0.5\cdot x_P + 1.125 \\
y_P &=\, p_2(x_P) = \tfrac 12 \cdot x_P^2 + 3 \\
\implies \qquad p_1(x_P) &= p_2(x_P) \\
\implies \qquad \tfrac 12 \cdot x_P^2 – 0.5\cdot x_P + 1.125 &= \tfrac 12 \cdot x_P^2 + 3 \\
\implies \qquad – 0.5\cdot x_P + 1.125 &= 3 \\
\implies \qquad – 0.5\cdot x_P &= 1.875 \\
\implies \qquad x_P &= -3.75\ \end{align}
Eingesetzt in \( p_2 \) erhalten wir
\begin{align} p_2(-3.75) &= \, \tfrac 12 \cdot(-3.75)^2 + 3\ &\approx \, 10.03. \end{align}
Der Schnittpunkt ist somit bei \((-3.75|10.03)\).
Zurück zum MAP-Hack:

Lösung zu B1.3
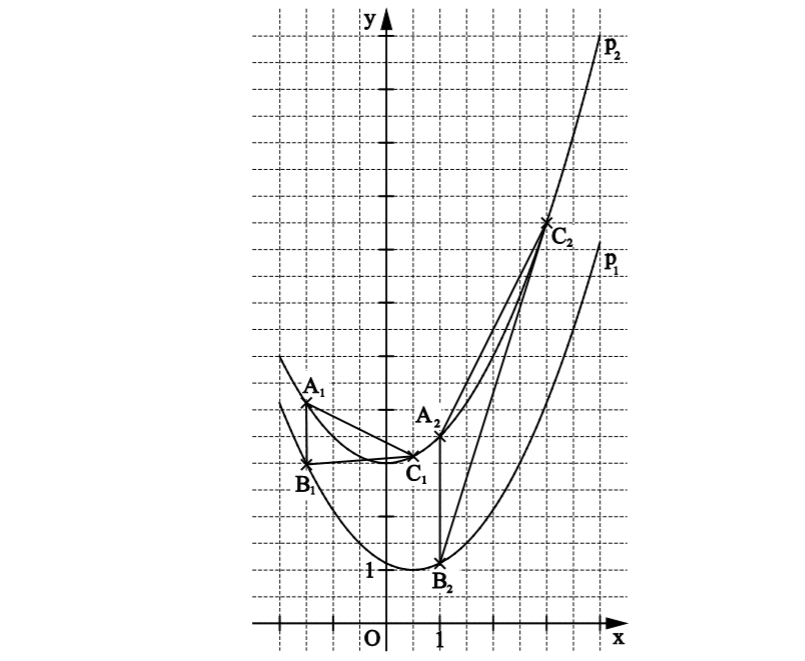
Zeichne zuerst die Dreiecke ein! Da gibt es schon den ersten Punkt =)
Stellen wir\(C_n\) dar als \(C_N = (x_C|y_C)\) und \(A_N\) als \(A_N= (x_A|y_A)\), so gilt \(x_C = x_A+2\), da die Abszisse von \(C_N\) immer um 2 größer sein soll als die der Punkte aus \(A_N\). Da \(C_N\) wie \(A_N\) auf der Parabel \(p_2\) liegen, setzen wir \(x_C\) in die Definition von \(p_2\) ein:
\begin{align} p_2(x_C) &= \,p_2(x_A + 2)\\
&= 0.5\cdot (x_A + 2)^2 + 3 \\
&= 0.5\cdot x_A^2 + 0.5 \cdot 2 \cdot 2\cdot x + 0.5 \cdot 2^2 + 3 \\
&= 0.5\cdot x_A^2 + 2 \cdot x_A + 5 \\
&= y_C. \end{align}
Also kann \(C_N\) dargestellt werden als \((x + 2|0.5\cdot x^2 + 2 \cdot x + 5)\).
Zurück zum MAP-Hack:

Lösung zu B1.4
Die Strecke \( [A_nB_n] \) berechnet sich aus der Differenz der \(y\)-Koordinaten, da die \(x\)-Koordinaten identisch, nämlich \(x\), sind:
\begin{align} A_nB_n &= \, \left(0.5\cdot x^2 + 3\right) – \left( 0.5 \cdot x^2 – 0.5 \cdot x + 1.125\right) \\
&= \, 0.5 \cdot x^2 + 3 \, – \, 0.5 \cdot x^2 + 0.5 \cdot x – 1.125 \\
&= \, (0.5 \cdot x + 1.875) \, LE. \end{align}
Zurück zum MAP-Hack:

Lösung zu B1.5
Um einen rechten Winkel an der Ecke \(B_3\) zu erhalten, müssen die Strecken \([A_3B_3]\) und \([B_3C_3]\) senkrecht aufeinander stehen. Da die \(x\)-Koordinate von \(A_n\) und \(B_n\) gleich ist, ist die Strecke \([A_nB_n]\) immer parallel zur \(y\)-Achse. Daher muss die Strecke \([B_3C_3]\) parallel zur \(x\)-Achse verlaufen. Das ist genau dann der Fall, wenn die \(y\)-Koordinaten von \(B_3\) und \(C_3 \) identisch sind:
\begin{align} y_{B_3} &= \, y_{C_3} \\
\implies \qquad 0.5 \cdot x^2 – 0.5\cdot x + 1.125 &= \, 0.5\cdot x^2 + 2\cdot x + 5 \\
\implies \qquad -2.5\cdot x &= \, 3.875 \\
\implies \qquad x &= \, -1.55. \end{align}
Eingesetzt in \(B_n\) erhalten wir
\begin{align} B_3 = \,B_n (-1.55) &= \left(-1.55 \,|\,0.5\cdot(-1.55)^2 – 0.5\cdot-1.55 + 1.125 \right) \\ &= (-1.55\,|\, 3.09). \end{align}
Zurück zum MAP-Hack:

Lösung zu B1.6
Auch hier nutzen wir wieder aus, dass die Strecke \([A_nB_n]\) immer parallel zur y-Achse ist. Die Mittelpunktschar zwischen [/latex]A_n[/latex] und \(B_n \) bezeichnen wir mit \(M_n\). Sie wird als Summe des halben Abstands zwischen den beiden Punkten und \(B_n\) im Bereich \([-3.75, \infty[ \) berechnet und hat die Koordinaten
\begin{align} M_n(x) &= \, \left(x \,| \, 0.5 \cdot x^2 – 0.5\cdot x + 1.125 + \tfrac 1 2\cdot(0.5 \cdot x + 1.875)\right) \\
&= \, \left(x \,| \, 0.5 \cdot x^2 – 0.25 \cdot x + 2.06\right). \end{align}
Die Punkte auf der Geraden, die zur \(x\)-Achse parallel ist und Abstand \(0.5 \cdot x^2 – 0.25 \cdot x + 2.06\) hat, bilden alle mit \(A_n\) und \(B_n \) gleichschenklige Dreiecke, da sie ja alle denselben Abstand zu \(A_n\) und \(B_n \) haben.
Damit \(A_4B_4C_4\) gleichschenklig wird, muss also \(C_4\) dieselbe \(y\)-Koodinate haben wie \(M_4\):
\begin{align} y_{M_4} &= \, y_{C_4}\\
\implies \qquad 0.5 \cdot x^2 – 0.25 \cdot x + 2.06 &= \, 0.5\cdot x^2 + 2\cdot x + 5\\
\implies \qquad – 2.25 \cdot x &= 2.94\\
\implies \qquad x &= -1.31. \end{align}
