
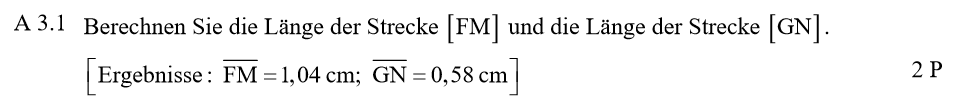
Lösung zu A3.1
Es gilt \( \sphericalangle BFE = \sphericalangle BFM\), da \(\sphericalangle FME = 180^\circ\). Berechnung von \(\overline{FM}\) über den Tangens von \(\sphericalangle BFM\)
\begin{align} \tan(\sphericalangle BFM) =& \; \frac{\;\overline{BM}\;}{\overline{FM}}\\
\Rightarrow \qquad\qquad \overline{FM} =& \; \frac{\overline{BM}} { \tan(\sphericalangle BFM)} \\
\Rightarrow \qquad\qquad \overline{FM} =& \; \frac{4,5 \text{ cm}}{ \tan(77^\circ)} \\
\Rightarrow \qquad\qquad \overline{FM} \approx& \; 1,04 \text{ cm} \end{align}
Da die Figur rotationssymmetrisch um die Achse \(\overline{BM}\) ist, gilt \( \overline{AN} = \overline{NC} = \tfrac 1 2 \cdot \overline {AC} = 2,5 \text{ cm}\). Daher ist auch \(\overline {BN} = 2,5 \text{ cm}\).
Weil \(\overline{AC}\) und \(\overline{FE}\) parallel sind, gilt \(\sphericalangle BGN = \sphericalangle BFM\) (Stufenwinkel). Damit kann \(\overline BN\) berechnet werden:
\begin{align} \tan(\sphericalangle BGN) =& \; \frac{\;\overline{BN}\;}{\overline{GN}}\\
\Rightarrow \qquad\qquad \overline{GN} =& \; \frac{\overline{BN} }{ \tan(\sphericalangle BGN) }\\
\Rightarrow \qquad\qquad \overline{GN} =& \; \frac{2,5 \text{ cm}}{\tan(77^\circ)} \\
\Rightarrow \qquad\qquad \overline{GN} \approx& \; 0,58 \text{ cm} \end{align}
Zurück zum MAP-Hack:
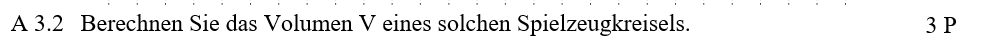
Lösung zu A3.2
Das Gesamtvolumen \(V_{\text{Kreisel}}\) setzt sich zusammen aus dem Volumen der Halbkugel \(V_{\text{Halbkugel}}\) und dem Volumen des Kegelstumpfes. Dieses wiederum lässt sich über das Volumen des gesamten Kegels \(V_{\text{KEGEL}}\) abzüglich des kleinen Kegels \(V_{\text{kegel}}\), der in der Halbkugel liegt, berechnen. Hinweise zur Rechnung:
Das Volumen der Halbkugel ist halb so groß wie das Volumen der vollen Kugel mit dem Mittelpunkt \(N\) und Radius \(\overline{AN}\),
Der große Kegel hat die Spitze in \(B\) und eine kreisförmigen Grundfläche mit dem Mittelpunkt in \(M\) und Radius \(\overline FM\).
Der kleine Kegel hat die Spitze in \(B\) und eine kreisförmigen Grundfläche mit dem Mittelpunkt in \(N\) und Radius \(\overline GN\).
Die einzelnen Volumina sind somit
\begin{align} V_{\text{Halbkugel}} &= \; \tfrac 1 2 \cdot \left( \tfrac 4 3 \cdot \pi \cdot \overline{AN}^3\right) \\ &= \; \tfrac 1 2 \cdot \tfrac 4 3 \cdot \pi \cdot (2,5\text{ cm})^3 \\ &\approx \; 32,72 \text{ cm}^3 \\ V_{\text{KEGEL}} &= \; \tfrac 1 3 \cdot \overline{FM}^2 \cdot \pi \cdot \overline{BM} \\ &= \; \tfrac 1 3 \cdot (1,04 \text{ cm})^2 \cdot \pi \cdot 4,5 \text{ cm}\\ &\approx \; 5,10 \text{ cm}^3 \\ V_{\text{kegel}} &= \; \tfrac 1 3 \cdot \overline{GN}^2 \cdot \pi \cdot \overline{BN} \\ &= \; \tfrac 1 3 \cdot (0,58 \text{ cm})^2 \cdot \pi \cdot 2,5 \text{ cm} \\ &\approx \; 0,88 \text{ cm}^3 \end{align}
Zusammengesetzt ist somit das Gesamtvolumen des Kreisels
\begin{align} V_{\text{Kreisel}} &= \; V_{\text{Halbkugel}} + V_{\text{KEGEL}} – V_{\text{kegel}}\\ &= \; 32,72 \text{ cm}^3 + 5,10 \text{ cm}^3 – 0,88 \text{ cm}^3\\ &= \; 36,94 \text{ cm}^3 \end{align}
