
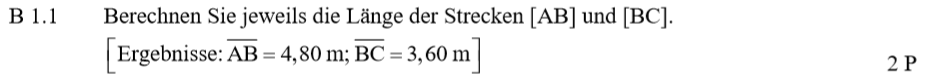
Lösung zu B1.1
\begin{align} &\overline{AB} \, \text{ mit dem Cosinus:}\\
cos(\angle BAC) &= \frac{\overline{AB}}{\overline{AC}} \,\,\, |cdot \overline{AC}\\
\overline{AB} &= cos(\angle BAC) \cdot \overline{AC} \\
&= 6,00 \cdot cos(36,87°)\\
\Rightarrow &\overline{AB}= 4,80 \text{m}\\
\\
&\overline{BC} \text{ mit dem Sinus:}\\
sin(\angle BAC) &= \frac{\overline{BC}}{\overline{AC}} \,\,\, |\cdot \overline{AC}\\
\overline{BC} &= \overline{AC} \cdot sin(\angle BAC)\\
&= 6,00 \cdot sin(36,87°)\\
\Rightarrow &\overline{BC} = 3,60 \text{m} \end{align}
Zurück zum MAP-Hack:

Lösung zu B1.2
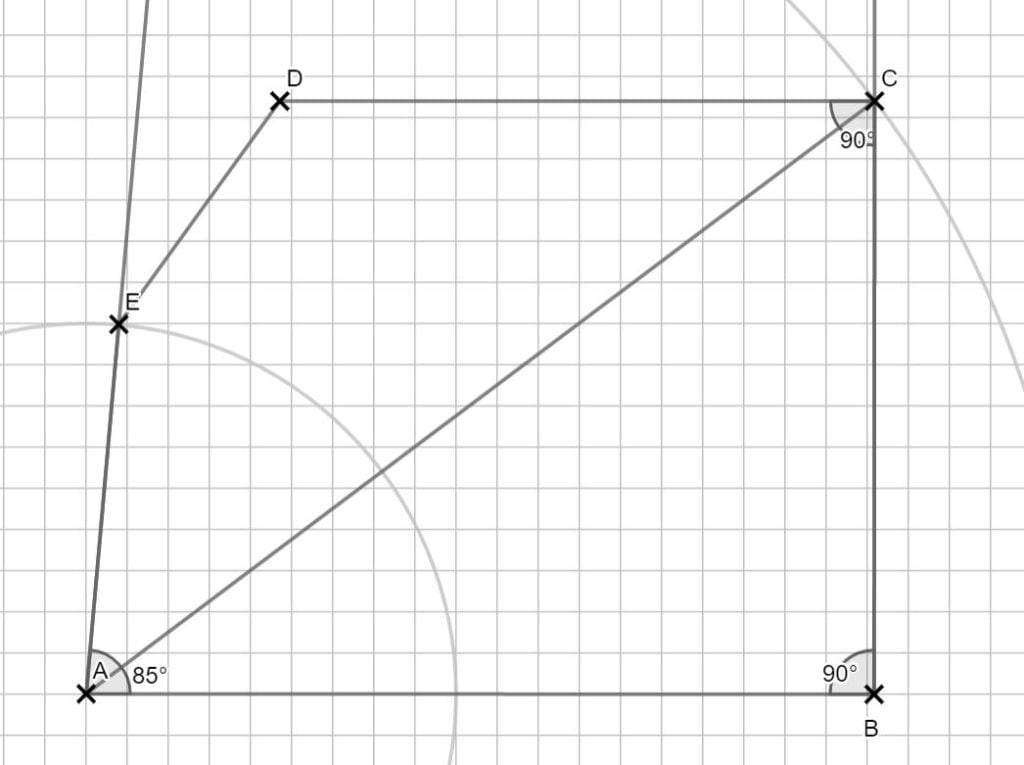
\( \angle DCA = \angle BAC \, \Rightarrow \, AB \, || \, CD \), weil es Wechselwinkel an parallelen Geraden sind.
Zurück zum MAP-Hack:

Lösung zu B1.3
Um \( \overline{EC} \) mit dem Cosinussatz zu bestimmen, benötigst du zuerst den Winkel CAE.
\begin{align} &\angle CAE \text{ über die Differenz:}\\
\angle CAE &= \angle BAE – \angle BAC\\
&= 85° – 36,87° \\
\Rightarrow &\angle CAE = 48,13° \\
\\
&\overline{EC} \text{ mit dem Cosnissatz:}\\
\overline{EC}^2 &= \overline{AE}^2 + \overline{AC}^2 – 2 \cdot \overline{AE} \cdot \overline{AC} \cdot cos(\angle CAE)\\
&= 2,25^2 + 6,00^2 -2 \cdot 2,25 \cdot 6,00 \cdot cos(48,13°)\\
\Rightarrow &\overline{EC}=4,80 \text{m} \end{align}
Jetzt wird es etwas schwieriger. Für \(\overline{ED}\) brauchst du den Winkel DCE. Für diesen brauchst du wiederrum den Winkel ECA. Diesen kannst du mit dem Sinussatz bestimmen:
\begin{align} &\angle ECA \text{ mit dem Sinussatz:} \\
\frac{sin(\angle ECA)}{\overline{AE}}&= \frac{sin(\angle CAE)}{\overline{EC}}\\
\frac{sin(\angle ECA)}{2,25} &= \frac{sin(48,13°)}{4,80} \,\,\, |\cdot 2,25 \\
sin(\angle ECA) &= \frac{sin(48,13°)}{4,80} \cdot 2,25\\
\Rightarrow &\angle ECA = 20,43° \\
\\
&\angle DCE \text{ über die Differenz:}\\
\angle DCE &= \angle DCA – \angle ECA\\
&= 36,87° – 20,43° \\
\Rightarrow &\angle DCE = 16,44°\\
\\
&\overline{ED} \text{ mit dem Cosinussatz:} \\
\overline{ED}^2 &= \overline{EC}^2 + \overline{CD}^2 – 2 \cdot \overline{EC} \cdot \overline{CD} \cdot cos(\angle DCE)\\
&= 4,80^2 + 3,60^2 -2 \cdot 4,80 \cdot 3,60 \cdot cos(16,44°)\\
\Rightarrow &\overline{ED} = 1,69 \text{m} \end{align}
Zurück zum MAP-Hack:

Lösung zu B1.4
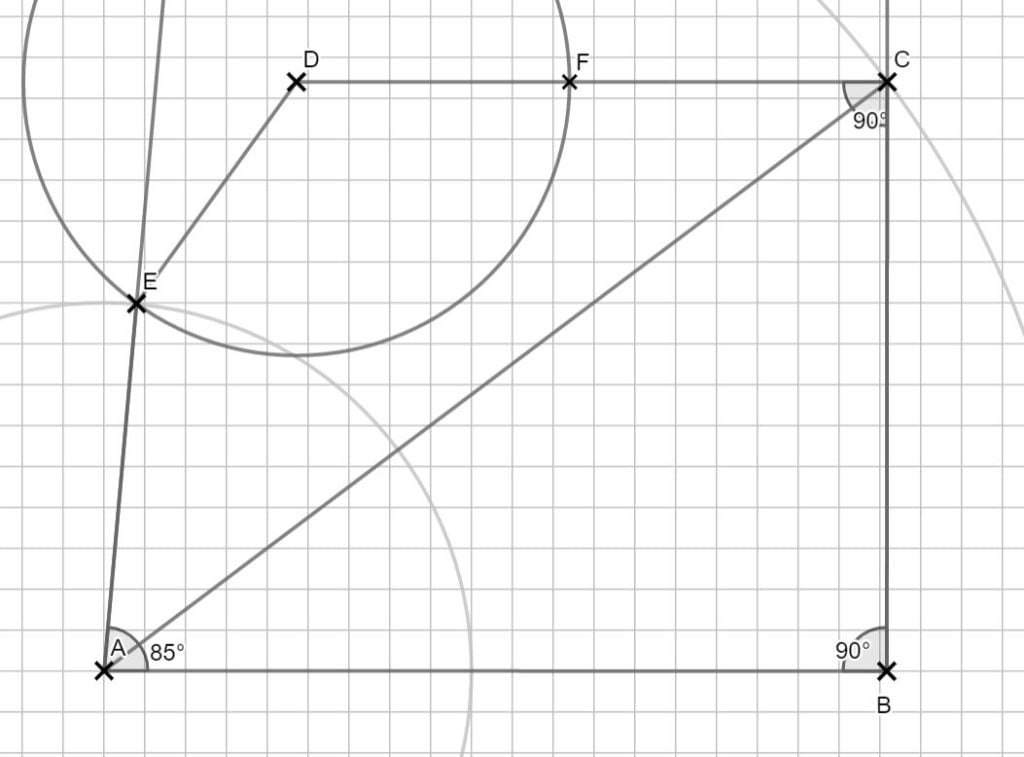
Einzeichnen des Kreisbogens wie in der Zeichnung.
\begin{align} &\angle EDF \text { mit dem umgeformten Cosinussatz:}\\
cos(\angle EDF) &= \frac{\, \overline{ED}^2 + \overline{CD}2 – \overline{EC}^2 \,}{2 \cdot \overline{ED} \cdot \overline{CD}}\\
&= \frac{1,69^2 + 3,60^2 – 4,80^2}{2 \cdot 1,69 \cdot 3,60}\\
\Rightarrow &\angle EDF = 126,42° \end{align}
Zurück zum MAP-Hack:

Lösung zu B1.5
Das Fünfeck setzt sich aus drei Dreiecken zusammen. Wir addieren die Flächeninhalte der Dreiecke und ziehen den Flächeninhalt es Kreissektors ab:
\begin{align} &A_{Fünfeck} \text{ über die Dreiecke:}\\
A &= A_{ABC} + A_{ACE} + A_{ECD} \\
&= 0,5 \cdot \overline{AB} \cdot \overline{BC} + 0,5 \cdot \overline{AC} \cdot \overline{AE} \cdot sin(\angle CAE) + 0,5 \cdot \overline{ED} \cdot \overline{CD} \cdot sin(\angle EDF) \\
&= 0,5 \cdot (4,8 \cdot 3,6 + 6 \cdot 2,25 \cdot sin(48,13°) + 1,69 \cdot 3,6 \cdot sin(126,42°)\\
\Rightarrow &A = 16,11 \text{m}^2 \\
\\
&A_{Sektor} \text{ über die Flächenformel:}\\
A_{Sektor} &= \frac{\angle EDF}{360°} \cdot \overline{ED}^2 \cdot \pi \\
&= \frac{126,42°}{360°} \cdot 1,69^2 \cdot \pi \\
\Rightarrow &A_{Sektor} = 3,15 \text{m}^2 \\
\\
&A_{Fließen} \text{ aus der Differenz:}\\
A_{Fließen} &= A – A_{Sektor}\\
&= 16,11 – 3,15 \\
\Rightarrow &A = 12,96 \text{m}^2 \end{align}
Zurück zum MAP-Hack:

Lösung zu B1.6

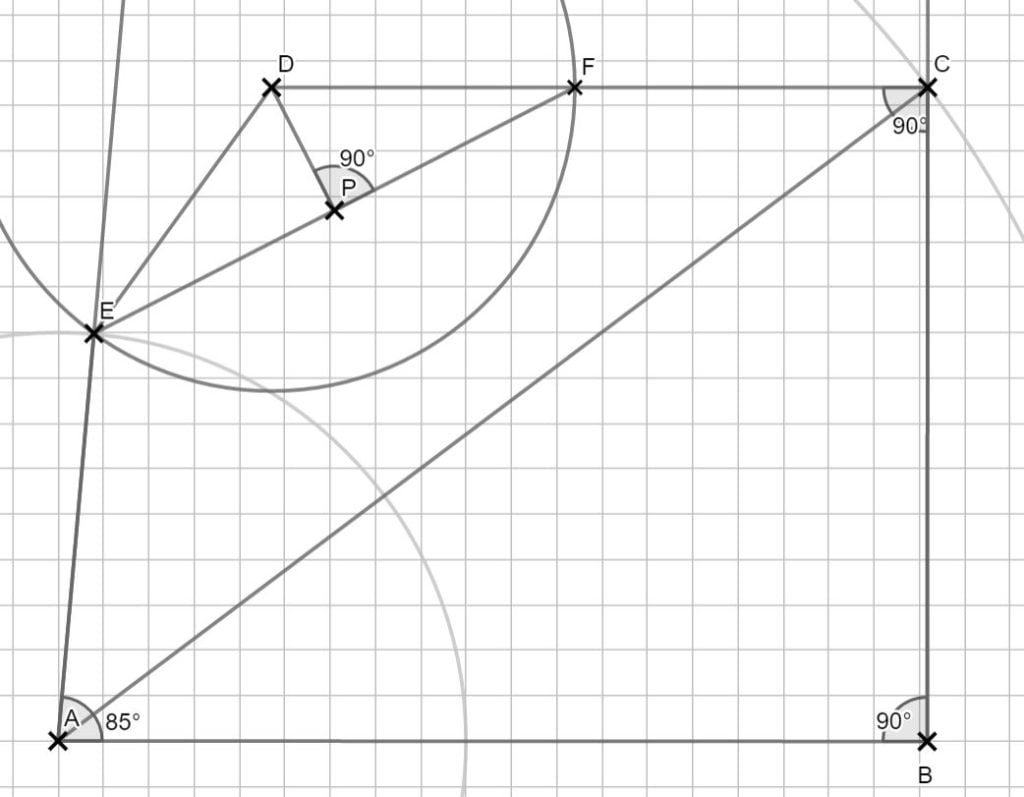
Weil im Punkt P die minimale Entfernung zu D ist, steht die Verbindungsstrecke [PD] hier senkrecht. Du kannst in diesen Dreiecken also z.B. den Cosinus benutzen:
\begin{align}
\angle EDP = 0,5 \cdot \angle EDF = 63,21° \\
\\
&\overline{PD} \text{ mit dem Cosinus:}\\
cos(\angle EDP} &= \frac{\overline{PD}}{\overline{ED}}\,\,\, |\cdot \overline{ED}\\
\overline{PD} &= \overline{ED} \cdot cos(63,21°)\\
\Rightarrow &\overline{PD} = 0,76 \text{m} \end{align}
