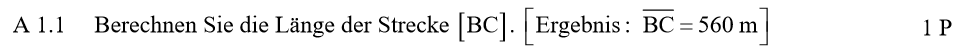
Lösung zu A1.1
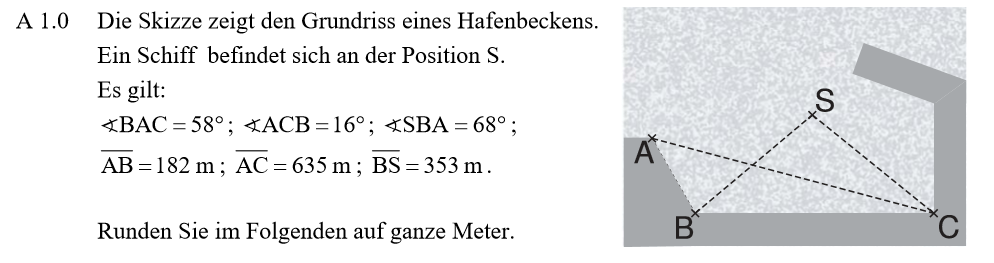
\begin{align} &\overline{BC} \, \text{mit dem Cosinussatz:} \\
\overline{BC}^2 &= \overline{AB}^2 + \overline{AC}^2 – 2 \cdot \overline{AB} \cdot \overline{AC} \cdot cos(\angle BAC) \\
\overline{BC}^2 &= 182^2 + 635^2 – 2 \cdot 182 \cdot 635 \cdot cos(58°) \\
\Rightarrow &\overline{BC} = 560 \text{m} \end{align}
Zurück zum MAP-Hack:
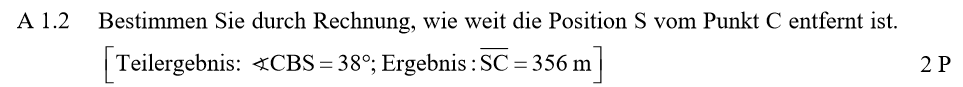
Lösung zu A1.2
\begin{align} &\angle CBA \, \text{über die Innenwinkelsumme:}\\
\angle CBA &= 180° – \angle BAC – \angle ACB \\
&= 180° – 58° – 16° \\
\Rightarrow &\angle CBA = 106° \\
\\
&\angle CBS \, \text{über die Differenz:}\\
\angle CBS &= \angle CBA – \angle SBA \\
&= 106° – 68° \\
\Rightarrow &\angle CBS = 38° \\
\\
&\overline{SC} \, \text{mit dem Cosinussatz:} \\
\overline{SC}^2 &= \overline{BS}^2 + \overline{BC}^2 – 2 \cdot \overline{BS} \cdot \overline{BC} \cdot cos (\angle CBS) \\
&= 353^2 + 560^2 – 2 \cdot 353 \cdot 560 \cdot cos(38°) \\
\Rightarrow &\overline{SC} = 356 \text{m} \end{align}
Zurück zum MAP-Hack:

Lösung zu A1.3
Weil im Punkt P der kleinste Abstand zu A sein soll, befindet sich dort ein rechter Winkel und du kannst im rechtwinkligen Dreieck ACP rechnen. Doch bevor du das machen kannst, musst nur noch den Winkel PCA bestimmen. Dafür brauchst du wiederum den Winkel SCB:
\begin{align} &\angle SCB \, \text{mit dem Sinussatz:} \\
\frac{sin(\angle SCB)}{\overline{BS}}&= \frac{sin(\angle CBS)}{\overline{SC}} \\
\frac{sin(\angle SCB)}{353} &= \frac{sin(38°)}{356} \,\,\,|\cdot 353 \\
sin(\angle SCB) &= \frac{sin(38°)}{356} \cdot 353 \\
\Rightarrow &\angle SCB = 37,62° \\
\\ &\angle PCA \, \text{über die Differenz:}\\
\angle PCA &= \angle SCB – \angle ACB\\
&= 37,62° – 16° \\
\Rightarrow &\angle PCA = 21,62°\\
\\
&\overline{AP} \, \text{mit dem Sinus:}\\
sin(\angle PCA) &= \frac{\overline{AP}}{\overline{AC}} \,\,\, |\cdot \overline{AC} \\
\overline{AP} &= sin(\angle PCA) \cdot \overline{AC} \\
&= sin(21,62°) \cdot 635 \\
\Rightarrow &\overline{AP} = 234 m \end{align}

Sehr geehrter Herr Cobanov,
könnten Sie bitte zur AP 2007 Aufgabe B Teil Ebene Geometrie die Lösungen und Schritte veröffentlichen.
Ihre Lösungen und Erklärungen finde ich sehr toll.
Ich bin leider im Fach Mathematik gar nicht gut und ich besuche die 10.Klasse. Vlt hätten Sie eine Lösung für mich. Besonders schwer ist das Thema Sinus Kosinus und Tangens für mich, ich versteh das nicht, wann mich was anwenden muss.
Ich hab von Ihnen als Übung auch die Mappe gekauft.
Ich hoffen Sie helfen mir dabei.
Ich wünsche Ihnen noch einen wunderschönen Tag und bleiben Sie gesund!
Mit freundlichen Grüßen
Hallo Christina,
danke für deinen netten Kommentar! Freut mich, dass dir der MAP-Hack hilft.
die Lösungen zu 2007 findest du hier: https://www.isb.bayern.de/realschule/leistungserhebungen/abschlusspruefungen-realschule/mathematik/2007/
Für die Auswahl des Ansatzes kannst du dir den Entscheidungsbaum im Ebene Geometrie-Hack anschauen – einfach bisschen runterscrollen: https://map-hack.de/ebene-geometrie/3
Falls es nur um Sinus, Cosinus und Tangens geht, da gibt es keine allgemeine Regel. Bestimmt hilft dir aber der Artikel zum Rechnen im rechtwinkligen Dreieck:
https://map-hack.de/grundwissen/rechtwinkliges-dreieck/
Hier sind auch Übungsaufgaben nur zum Rechnen im rechtwinkligen Dreieck.
Ich wünsche dir ein erholsames Wochenende! Falls es Fragen gibt, melde dich einfach!
Tobias Cobanov