Quadratische Funktionen
2.1
Weil der Scheitelpunkt gegeben ist, setzt du mit der Scheitelform an. Aus der gegebenen Funktionsgleichung kannst du außerdem ablesen, dass der Öffnungsfaktor a = -0,4 ist.
\begin{align} &\text{Einsetzen in die Scheitelform:}\\
y &= a \cdot (x – x_S)^2 + y_S \,\,\, \text{ mit a = -0,4 und S(1|3)}\\
&= -0,4 \cdot (x – 1)^2 +3 \\
&= -0,4 \cdot (x² -2x + 1) + 3 \\
&= -0,4x² + 0,8x + 2,6 \end{align}
2.2 + 2.3
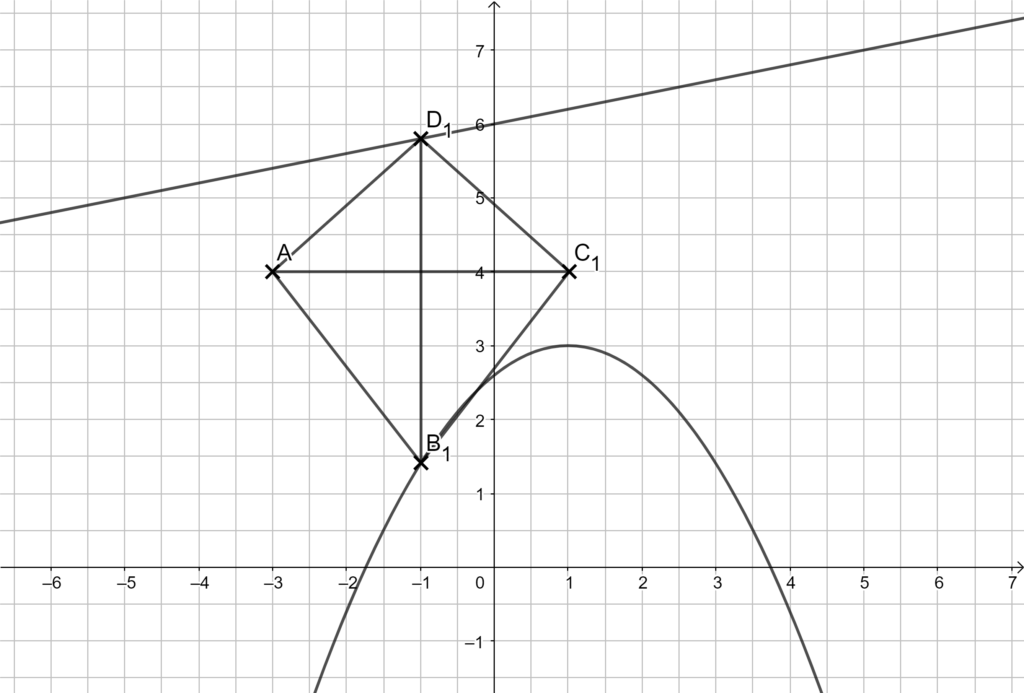
2.4
Die Gerade un die Parabel haben keine Schnittpunkte. Du kannst also keine Schnittpunkte der Funktionen bestimmen.
Hier kommt das Problem mit den Bezeichnungen ins Spiel. Liegt die Diiagonale BD rechts vom Punkt A, dann heißt das Viereck ABCD.
Liegt die Diagonale aber links von A, dann spiegelt es den Punkt C auf die andere Seite und das Viereck heißt ADCB, was nicht erlaubt ist.
Die Diagonale muss also rechts von A liegen und es gilt: x > -3 .
2.5
Die Punkte B und D haben dieselbe Abszisse, also kannst du ihre Streckenlänge durch „Oben- Unten“ bestimmen:
\begin{align} |\overline{B_n D_n}| &= y_{Gerade} – y_{Parabel} \\
&= 0,2x + 6 – (-0,4x² +0,8x + 2,6) \\
&= 0,2x + 6 + 0,4x² – 0,8x – 2,6\\
&\Rightarrow |\overline{B_n D_n}| = (0,4x² – 0,6x + 3,4) LE \end{align}
2.6
Um die Aufgabe zu lösen, setzen wir die Diagonalenlängen gleich und lösen die Gleichung. Die Diagonale \(|\overline{B_n D_n}|\) kennst du aus 2.5, bleibt \(|\overline{A C_n}|\) zu bestimmen.
Weil A die x-Koordinate -3 hat und die andere Diagonale bei x liegt, ist der Abstand von A zu \(|\overline{B_n D_n}|\) immer x + 3.
Die volle Diagonale ist dann das Doppelte: \( |\overline{AC_n}|= 2x + 6 \) .
\begin{align} |\overline{B_n D_n}| &= |\overline{AC_n}| \\
0,4x² -0,6x + 3,4 &= 2x + 6 \,\,\, |-2x – 6 \\
0,4x² – 2,6x – 2,6 &= 0 \\
&\Rightarrow \text{Taschenrechner:} \, x_1 = 7,38 \, ; \, x_2 = -0,88 \end{align}
2.7
Der Winkel bei D ist genau dann 90°, wenn D auf einem Thaleskreis über AC liegt. Für den Radius des Thaleskreis gilt dann:
\( r = |\overline{AM_n}| = |\overline{DM_n}| = |\overline{CM_n}| \text{ mit } M_n\) der Schnittpunkt der Diagonalen.
Die Länge der Strecke \(|\overline{DM_n}|\) erhältst wenn, wenn du von der y-Koordinate des Punktes D die y-Koordinate von A abziehst.
Es ist eigentlich derselbe Trick wie in 2.6, nur dass man entlang der y-Achse rechnen muss. Es entsteht eine „normale“ lineare Gleichung, die du per Hand lösen kannst.
\begin{align}
\overline{AM_n} &= \overline{Dn M_n} \\
x + 3 &= (0,2x + 6) – 4 \,\,\, |-0,2x \\
0,8x +3 &= 2 \,\,\, |-3 \\
0,8x &= -1 \,\,\, |:0,8 \\
x &= -1,25 \end{align}
Für x = -1,25 ist der Winkel bei D 90°.
Ebene Geometrie
2.1
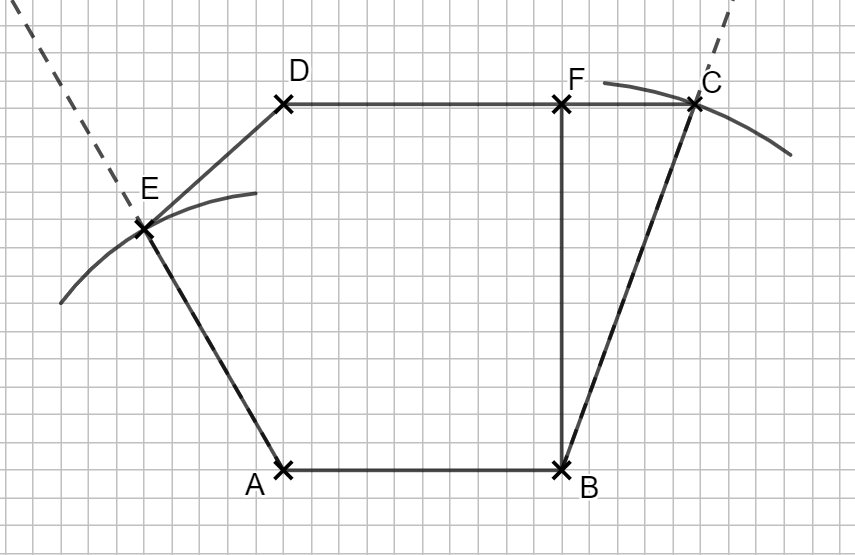
2.2
\begin{align} &\text{Berechnung von: } |\overline{BF}| \text{ mit dem Cosinus:}\\
cos(\angle CBF) &= \frac{|\overline{BF}|}{|\overline{BC}|} \\
cos(110° – 90°) &= \frac{|\overline{BF}|}{7} \,\,\, |\cdot 7 \\
&\Rightarrow |\overline{BF}| = cos(20°) \cdot 7 = 6,58 \text{cm}\end{align}
2.3
Im Dreieck AED hast du zwar drei Angaben, aber leider kannst du den Winkel bei E nicht direkt berechnen. Zuerst musst du über einen Zwischenschritt die Streckenlänge \( |\overline{ED}|\) bestimmen.
Diese Streckenlänge ist auch als Zwischenergebnis angegeben. Die Aufgabe verrät dir also den Lösungsweg.
\begin{align} &|\overline{ED}| \text{ mit dem Cosinussatz:}\\
|\overline{ED}|^2 &= |\overline{AE}|^2 + |\overline{AD}|^2 – 2 \cdot |\overline{AE}| \cdot |\overline{AD}| \cdot cos(\angle EAD) \\
&= 5^2 + 6,58^2 – 2 \cdot 5 \cdot 6,58 \cdot cos(120° – 90°) \,\,\, |\sqrt{}\\
&\Rightarrow |\overline{ED}| = 3,36 \text{cm} \\
\\
&\angle AED \text{ mit dem Sinussatz:}\\
\frac{sin(\angle AED)}{|\overline{AD}|} &= \frac{sin(\angle EAD)}{|\overline{ED}|} \\
\frac{sin(\angle AED)}{5} &= \frac{sin(30°)}{3,36} \,\,\, |\cdot 5 \\
sin(\angle AED) &= \frac{sin(30°)}{3,36} \cdot 5 \,\,\, |sin^{-1}\\
&\Rightarrow \angle AED = 48,08° \end{align}
2.4
Das Fünfeck setzt sich aus dem Dreieck ADE, dem Rechteck ABFD und dem Dreieck BCF zusammen. Du berechnest die einzelnen Teilflächen und addierst dann.
\begin{align}
A_{ADE} &= 0,5 \cdot |\overline{AE}| \cdot |\overline{AD}| \cdot sin(\angle DAE) \\
&= 0,5 \cdot 5 \cdot 6,58 \cdot sin(30°) \\
&\Rightarrow A_{ADE} = 8,23 \text{cm}^2 \\
\\
A_{ABFD} &= |\overline{AB}| \cdot |\overline{AD}| \\
&= 5 \cdot 6,58 \\
&\Rightarrow A_{ABFD} = 32,9 \text{cm}^2 \\
\\
A_{BCF} &= 0,5 \cdot |\overline{BC}| \cdot |\overline{BF}| \cdot sin(\angle CBF) \\
&= 0,5 \cdot 7 \cdot 6,58 \cdot sin(20°) \\
&\Rightarrow A_{BC} = 7,88 \text{cm}^2 \\
\\
A_{ABCDE} &= A_{ADE} + A_{ABFD} + A_{BCF} \\
&= 8,23 + 32,9 + 7,88 \\
&\Rightarrow A_{ABCDE} = 49,01 \text{cm}^2 \end{align}
2.5 Einzeichnen des Kreisbogens
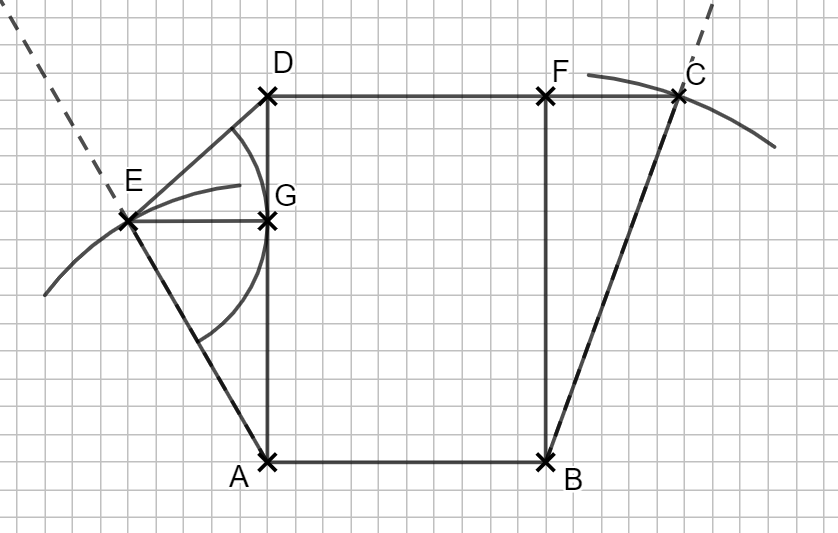
Um den Flächeninhalt berechnen zu können, benötigst du den Radius \( |\overline{EG}| \). Weil der Kreis die Strecke \( \overline{AD}\) berührt, steht der Radius senkrecht auf dieser Strecke. Du kannst im Dreieck AGE also mit Sinus, Cosinus, Tangens und dem Satz des Pythagoras rechnen.
\begin{align} &|\overline{EG}| \text{ mit dem Sinus:}\\
sin(\angle DAE) &= \frac{|\overline{EG}|}{|\overline{AE}|} \\
sin(30°) &= \frac{|\overline{EG}|}{5} \,\,\, |\cdot 5 \\
&\Rightarrow |\overline{EG}| = sin(30°) \cdot 5 = 2,5 \text{cm}\\
\\
&\text{Berechnung des Flächeninhalts:}\\
A &= \frac{\angle AED}{360°} \cdot |\overline{EG}|^2 \cdot \pi \\
&= \frac{48,08°}{360°} \cdot 2,5^2 \cdot \pi \\
&\Rightarrow A = 3,98 \text{ cm}^2 \end{align}
