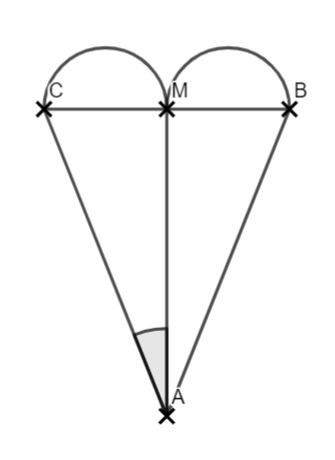
A1 Die nebenstehende Skizze zeigt eine achsensymmetrische Figur ABC mit Symmetrieachse AM, die durch zwei Halbkreisbögen und die Strecken \( \overline{AB} \text{ und } \overline{AC} \) begrenzt wird.
Es gilt: \( \angle MAC = 30° ; |\overline{AM}|= 6 cm \)
Berechnen Sie den Flächeninhalt der Figur.
(Tipp: \( 12 \sqrt{3} + 3 \pi = 30,21 cm^2 )\)
Lösung zu A1
Die Figur setzt sich aus zwei kongruenten Dreiecken und zwei Halbkreisen zusammen. Für beide Figuren benötigst du die Streckenlänge von \( \overline{CM} \). Weil die Figur achsensymmetrisch ist, ist bei M ein rechter Winkel und du kannst im Dreieck AMC die gesuchte Strecke berechnen. Die Hälfte von \( \overline{CM} \) ist dann der Radius des Kreises. Man könnte auch einen Halbkreis ausrechnen und dann mal 2 nehmen oder einfach gleich die „normale“ Kreisformel verwenden.
\begin{align} tan{\angle MAC} &= \frac{|\overline{CM}|}{|\overline{AM}|} \\
tan(30°) &= \frac{|\overline{CM}|}{6} \,\,\, |\cdot 6 \\
tan(30°) \cdot 6 &= |\overline{CM}| \,\,\,\,\,\, \text{Tabelle: } tan(30°) = \frac{\sqrt{3}}{3}\\
\frac{\sqrt{3}}{3} \cdot 6 &= |\overline{CM}| \,\,\,\,\,\, \text{6 mit der 3 kürzen} \\
\Rightarrow &|\overline{CM}| = 2\sqrt{3} \\
\\
&\text{A des Dreiecks ACM:}\\
A_{ACM} &= 0,5 \cdot |\overline{CM}| \cdot |\overline{AM}| \\
&= 0,5 \cdot 2\sqrt{3} \cdot 6 \\
\Rightarrow &A_{ACM} = 6\sqrt{3} \\
\\
&\text{A des Kreises:}\\
r &= |\overline{CM}| : 2 = 2\sqrt{3} :2 = \sqrt{3} \\
A_{Kreis} &= \pi \cdot r^2 \\
&= \pi \cdot \sqrt{3}^2 \\
\Rightarrow &A_{Kreis} = 3 \pi \\
\\
&\text{Zusammensetzen zum Gesamtergebnis}\\
A_{ges} &= A_{Kreis} + 2 \cdot A_{ACM} \\
&= 3 \pi + 2 \cdot 6 \sqrt{3} \\
&= 3 \pi + 12 \sqrt{3} \,\,\,\,\,\, \text{Tipp verwenden} \\
\Rightarrow &A_{ges} = 30,21 cm^2 \end{align}
