Der besprochene Taschenrechner ist der Typ Casio fx-991DE X .
Allgemeines
Der Taschenrechner besitzt 13 verschieden Menüs, die über die Taste Menü links des On-Buttons angezeigt werden.
Die normalen Berechnungen machst du im Menü 1: Berechnungen. Ist etwas seltsam oder du verstehst die Anzeige nicht, mache den Taschenrechner aus und an und starte einfach in Menü 1: Berechnungen von vorne.
Menü 1: Berechnungen
Allgemeines:
Hier sollte eigentlich alles klar sein! Jede Taste hat drei Funktionen, die über den normalen Tastendruck (weißer Text), über Shift (gelber Text) oder über Alpha (roter Text) angesteuert werden können. Der Taschnenrechner unterscheidet ein Vorzeichen (-) von dem Rechenzeichen -, aber das ist für uns egal. Verwende einfach immer das Minus rechts vom Plus.

Eine der wichtigsten Tasten ist „S<=>D“ überhalt von Delete. Es wechselt die Darstellung zwischen der wissenschaftlichen (scientific) Bruchdarstellung und der Dezimaldarstellung (decimal). Kurz gesagt: Es wechselt zwischen Bruch und Dezimalzahl.
Das kannst du auch immer verwenden, wenn du zu einer Dezimalzahl einen passenden Bruch oder andersherum suchst.
Lineare Gleichungen lösen
Eine lineare Gleichung, also eine Gleichung bei der die höchste Potenz der x-Terme 1 ist, kann direkt von deinem Taschenrechner gelöst werden. Nehmen wir ein Beispiel für eine lineare Gleichung: \( 3x + 4 \cdot (0,5x – 4) = 0,5 \cdot (1,5x – 2) \).
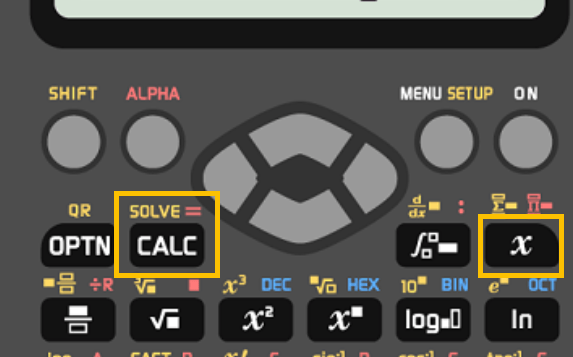
Du gibst die Gleichung ein, wobei du das x der Taste oben rechts verwendest und das Zeichen „=“ über Alpha + Calc oben links erhälst.
Ist die Rechnung komplett eingegeben, löst du die Gleichung durch Shift+Calc \( \Rightarrow \) Solve. Ja, die Taste Solve löst die Gleichung.
Aber nicht sofort! Jetzt wird das letzte Ergebnis angezeigt, das du mit dem Taschenrechner berechnet hast. Warum kann ich auch nicht erklären. Erst wenn du nochmal auf „=“ drückst erscheint die Lösung „x = 3,529…“. Gerundet ist das Ergebnis also x = 3,53.
Die untere Zeile „L-R = 0“ ist nur eine Bestätigung, dass die linke Seite und die rechte Seite der Gleichung gleich sind.
Zusammengefasst: Gleichung eingeben mit x und dem = über die Taste Calc und dann mit Shift+SOLVE lösen. Am Ende „=“-Drücken nicht vergessen und die Gleichung ist gelöst.
Variablen und Konstanten
Die roten Buchstaben sind Speicher für Zwischenergebnisse. Du kannst dir ein Ergebnis über die Tasten STO (store) überhalb der 7 und anschließendem Buchstaben dort speichern. Wenn also dann den roten Buchstaben einfügst, steht dieser für die hinterlegte Zahl. Das Ergebnis der letzten Rechnung speichert der Taschenrechner bei der Taste Ans (Answer.)
Wichtig ist der Unterschied zwischen dem roten x und dem weißen x in der oberen rechten Ecke. Wenn du eine Variable einer Funktion eingeben möchtest, verwende sicherheitshalber immer die Taste oben rechts. Es geht shcneller und macht in Spezialfällen keine Probleme.
Über Shift 7 bzw Shift 8 kannst du dir physikalsiche Einheiten umrechnen bzw. physikalsiche Konstanten einfügen.. Das klingt praktisch, ist es aber für die Abschlussprüfung nicht. Wenn es dir interessiert, schau einfach mal rein.
Menü 9: Tabellen
Ja, die Tabellen 2 – 8 sind für uns nicht wichtig. Im Menü 9 kannst du dir Tabellen für Funktionen erzeugen lassen. Der Taschenrechner fragt mit „f(x) = …“ nach dem Funktionsterm, für den eine Tabelle erstellt werden soll. Möchtest du z.B. die Funktion mit dem Term \( y= 2\cdot x^2 + 3\cdot x – 2 \) zeichnen, gibst du diesen ein und bestätigst die Eingabe – wie immer – mit dem Ist-Gleich.
In der Tabellenfunktions kann man immer gleich zwei Funktionen anzeigen lassen, deshalb zeigt der Taschenrechner „g(x) = …“ an. Diesen Schritt übergehst du einfach mit einem Ist-Gleich.
Start und Ende fragt nach dem Intervall für x. Wenn das Koordinatensystem der Aufgabe z.B. \( x \in [-3; 7] \) lautet, dann ist Start: -3 und Ende: 7. Inkre steht für Inkrement und um eine längere Geschichte abzukürzen: Das sind die Schritte in der Tabelle. Willst du „1er-Schritte“ in der Tabelle ist Inkre 1, willst du -3; -2,5 ; -2, .. , also halbzahlige Schritte, dann ist Inkre 0,5.
Es gibt Lehrer, die bestehen auf Schrittweite 0,5, vielen ist es aber auch egal. Frage einfach mal, ob Inkre 1 zum Zeichnen reicht.
Ein Ist-Gleich später steht die Tabelle da, aber Achtung!
Die erste Spalte ist die Zeilennummerierung und hat nichts mit deiner Funktion zu tun!
Die Eintragungen in der Tabelle sind die Punkte, die du ins KoSy eintragen musst. Hier sind die ersten Punkte also (1|3), (2|12), (3|25), …
Dieses Vorgehen kannst du in diesen beiden MAP-Hacks üben:
Und das war es auch schon mit diesem Menü. Viel Spaß mit den Punkten in der Abschlussprüfung!
Menü A: Gleichung/Funkt
Im Menü A: Gleichung/Funkt lassen sich Gleichungen untersuchen. Wählst du das Menü aus, wird zuerst gefragt, ob du ein Gleichungssystem oder eine Polynomgleichung lösen möchtest.
Ein Gleichungssystem besteht aus zwei Gleichungen und es gibt zwei Variablen, meistens x und y.
Eine Polynomgleichung hat nur eine Variable, meistens x, aber die Potenz beim x darf unterschiedlich sein. Hier kannst du quadratrische Gleichungen lösen.
1: Gleichungssysteme
Zuerst musst du die Anzahl an Variablen angeben. In der Abschlussprüfung kommen nur Gleichungssysteme mit 2 Variablen vor. Du wählst bei „Anzahl der Unbekannten? 2 – 4“ immer 2.
Wir besprechen am Beispiel
\begin{align} (I) \, \, 5x &= 2y \\
(II)\, \, 8x + y – 3 &= 0 \end{align}
Dass der Taschenrechner das Gleichungssystem lösen kann, musst du jede Gleichung so umformen, dass die Konstanten auf einer Seite und die Variablen auf der anderen Seite stehen. Falls du diesen Satz jetzt nicht verstehst, dann gibt es trotzdem Hoffnung. Der Taschenrechner zeigt dir genau die Form an, die er von dir verlangt:
\begin{align} 0 \cdot x + 0 \cdot y &= 0 \\
0 \cdot x + 0 \cdot y &= 0 \end{align}
Wir stellen unsere Gleichungen mit Äquivalenzumformungen um:
\begin{align}
(I) \, \, 5x &= 2y \,\,\ |-2y \\
\Rightarrow &(I) \, \, 5x – 2y = 0 \\
\\
(II) \, \, 8x + 1y – 3 &= 0 \,\,\, +3 \\
\Rightarrow &(II)\, \, 8x + y = 3 \end{align}
Für jede Null setzt du die Zahl der Aufgabe ein und lässt den Taschenrechner das GLS lösen. Steht keine Zahl vor der Variable, gilt der Wert 1.
Weil ein Gleichungssystem zwei Variablen hat, besteht die Lösung auch aus zwei Teilen, dem x und dem y. Zusammen bilden sie einen Punkt. Hier ist die Lösung \( (x|y) = (\frac{2}{7} | \frac{5}{7}) \)
Gleichungssysteme musst du nur beim Berechnen der Parabelgleichung aus zwei Punkten beherrschen. Das kannst du hier üben:
2: Polynom-Gleichungen
Im Menü Polynomgleichungen kannst du quadratische Gleichungen lösen. Der Taschenrechner fragt nach dem Polynom-Grad der Gleichung, also der höchsten Potenz bei der Variablen x. Weil du nur quadratische Gleichungen lösen muss, ist die Eingabe hier immer 2.
Um ein quadratische Gleichung zu löse, musst du sie immer auf die Form \( a \cdot x^2 + b \cdot x + c = 0 \) bringen. Wir machen ein Beispiel:
\begin{align} (x – 3)^2 + 3x &= 4 \\
x^2 – 6x +9 +3x &= 4 \\
x^2 – 3x + 9 &= 4 \,\,\, |-4 \\
x^2 -3x +5 = 0 \end{align}
Die Klammern wurden mit einer binomischen Formel aufgelöst, zusammenfasst und die Gleichung auf die Form „= 0“ gebracht. Jetzt kannst du einfach die Koeffizienten in den Taschenrechner eingeben und die die Lösung anzeigen lassen. Steht keine Zahl da, wie hier beim x², dann schreibe eine 1.
Der Taschenrechner gibt verschiedene Lösungen aus. Zuerst kommen die Nullstellen \( x_1 \) und \( x_2 \) der Parabel. Diese können, wie hier, ein komischer Bruch mit einem i sein. In diesem Fall gibt es keine Nullstelle oder anders formuliert: Es gibt keine Lösung für die Gleichung! Es ist auch möglich, dass es nur eine Lösung für die Gleichung gibt, dann nennt der Taschenrechner die Lösng einfach x, anstatt sie mit \( x_1 \) und \( x_2 \) zu nummieren.
Wichtig ist, dass du erkennt, ob es eine, zwei oder keine Lösungen gibt.
Anschließend zeigt der Taschenrechne, ob die quadratische Funktion ein Maximum oder ein Minimum hat und gibt den Scheitelpunkt aus. Dieser ist hier \( S(1,5 \, | \, 2,75) \).
Mit quadratischen Gleichungen muss man – Überraschung, Überraschung – bei quadratischen Funktionen arbeiten. Im verlinkten MAP-Hack kannst du üben:
Funktionen des Taschenrechners – Erklärt von Black Sheep Teaching
Christian Schäfer hat auf seinem Youtube-Kanal eine ganze Reihe an Erklärvideos zu diesem Taschenrechner. Schau doch einfach mal rein und hinterlasse ihm einen Kommentar und like, wenn es dir gefällt!
