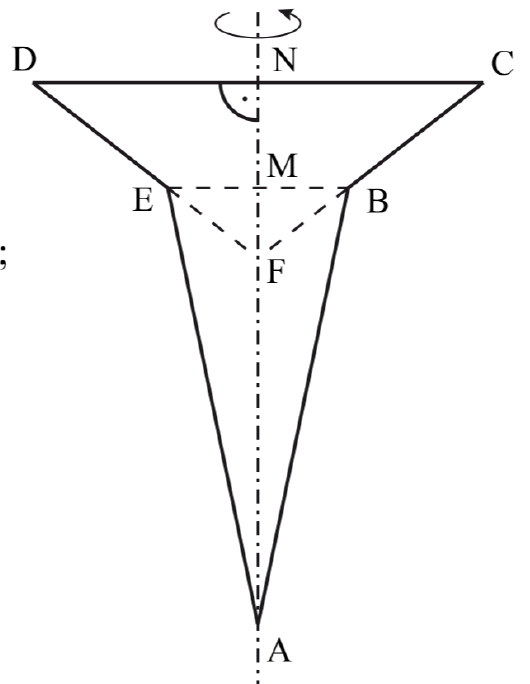
1.0 Ein Schreiner Stellt einen Holzkreisel für Kinder her. Die nebenstehende Skizze zeigt den Axialschnitt ABCDE des Kreisels mit AN als Symmetrieachse.
Es gilt:
Runden sie im Folgenden auf eine Stelle nach dem Komma.
1.1 Berechnen Sie die Längen der Strecken \( \overline{CD} \, \text{und} \, \overline{EM} \).
[Ergebnis: \( |\overline{CD}| = 15,0 cm ; |\overline{EM}| = 3,0 cm \) ]
Lösung zu 1.1
Weil die Figur achsensymmetrisch ist, gilt \(|\overline{DF}| = |\overline{CF}| = 9,5 \text{cm} \). Mit dem Winkel bei F hast du alles für den Cosinus-Satz zusammen.
\begin{align} &|\overline{CD}| \text{ mit Cosinussatz:}\\
|\overline{CD}|^2 &= |\overline{DF}|^2 +|\overline{CF}|^2 – 2 \cdot |\overline{DF}| \cdot |\overline{CF}| \cdot cos(\angle CFD) \\
&= 9,5^2 + 9,5^2 – 2 \cdot 9,5 \cdot 9,5 \cdot cos(104°) \,\,\, |\sqrt{}\\
&\Rightarrow |\overline{CD}| = 15,0 cm \\
\\
&|\overline{EM}| \text{ mit dem Sinus:}\\
sin(\frac{\angle CFD}{2} ) &= \frac{|\overline{EM}|}{|\overline{EF}|} \,\,\, |\cdot |\overline{EF}| \\
|\overline{EM}| &= sin(\frac{\angle CFD}{2}) \cdot |\overline{EF}| \\
&= sin(52°) \cdot 3,8 \\
&\Rightarrow |\overline{EM}| = 3,0 \text{cm} \end{align}
1.2 Berechnen Sie das Volumen des Kreisels.
Lösung zu 1.2
Das gesuchte Volumen setzte sich aus dem Kegelstumpf (im Schrägbild) BCDE und dem Kegel (im Schrägbild) ABE zusammen. Ein Kegelstumpf berechnest du immer, indem du vom großen Kegel (FCD) den kleinen Kegel (FBE) abziehst.
Diese drei Bausteine musst du berechnen. Für den großen Kegel brauchst du noch die Höhe \( |\overline{NF}| \) bzw. \( |\overline{MF}| \) , den Rest kennst du schon.
\begin{align} &|\overline{NF}| \text{ bzw. } |\overline{MF}| \text{ mit dem Cosinus:}\\
cos(\angle NFD) &= \frac{|\overline{NF}|}{|\overline{DF}|} \,\,\, |\cdot |\overline{DF}| \\
|\overline{NF}| &= cos(\angle NFD) \cdot |\overline{DF}| \\
&= cos(52°) \cdot 9,5 \,\,\, |cos^{-1}\\
&\Rightarrow |\overline{NF}| = 5,8 \text{cm} \\
cos(\angle MFD) &= \frac{|\overline{MF}|}{|\overline{EF}|} \,\,\, |\cdot |\overline{EF}| \\
|\overline{MF}| &= cos(\angle MFD) \cdot |\overline{EF}| \\
&= cos(52°) \cdot 3,8 \,\,\, |cos^{-1}\\
&\Rightarrow |\overline{MF}| = 2,3 \text{cm} \\
\\
&\text{Allgemeine Flächenformel:}\\
V_{Kegel} &= \frac{1}{3} \cdot \pi \cdot r^2 \cdot h\\
\\
V_{FCD} &= \frac{1}{3} \cdot \pi \cdot |\overline{DN}|^2 \cdot |\overline{NF}| \\
&= \frac{1}{3} \cdot \pi \cdot 7,5^2 \cdot 5,8 \\
&\Rightarrow V_{FCD} = 341,6 \text{cm}^3\\
\\
V_{FBE} &= \frac{1}{3} \cdot \pi \cdot |\overline{EM}|^2 \cdot |\overline{MF}| \\
&= \frac{1}{3} \cdot \pi \cdot 3^2 \cdot 2,3 \\
&\Rightarrow V_{FBC} = 21,7 \text{cm}^3\\
\\
V_{ABE} &= \frac{1}{3} \cdot \pi \cdot |\overline{EM}|^2 \cdot |\overline{AM}|\\
&= \frac{1}{3} \cdot \pi \cdot 3^2 \cdot 14,5 \\
&\Rightarrow V_{ABE} = 136,7 \text{cm}^3\\
\\
V_{ges} &= V_{FCD} – V_{FBE} + F_{ABE} \\
&= 341,6 – 21,7 + 136,7 \\
&\Rightarrow V_{ges} = 456,6 \text{cm}^3 \end{align}
1.3 Der Kegel, der durch Rotation des Dreiecks EAB an der Achse AN entsteht, soll in roter Farbe bemalt werden.
Der Rest wird in weiß gestrichen. Berechnen Sie die Oberfläche der weißen Fläche.
Lösung zu 1.3
Die gesuchte Oberfläche setzt sich aus einer Kreisfläche und dem Mantel des Kegelstumpfes zusammen. Für die Mantelfläche ziehen wir vom großen Kegel den kleinen Kegel ab.
\begin{align} &O_{EFM} \text{ über die Flächenformel:}\\
M_{EFM} &= s \cdot \pi \cdot r \\
&= |\overline{EF}| \cdot \pi \cdot |\overline{MF}| \\
&= 3,8 \cdot \pi \cdot 3,0 \\
\Rightarrow &M_{EFM} = 35,8 cm^2 \\
\\
&M_{DFN} \text{ über die Flächenformel:}\\
M_{DFN} &= s \cdot \pi \cdot r \\
&= |\overline{DF}| \cdot \pi \cdot |\overline{ND}| \\
&= 9,5 \cdot \pi \cdot 7,5 \\
\Rightarrow &M_{EFM} = 223,8 cm^2 \\
\\
&A_{Kreis} \text{ über die Flächenformel:} \\
A_{Kreis} &= r^2 \cdot \pi \\
&= |\overline{DN}|^2 \cdot \pi \\
&= 7,5^2 \cdot \pi\\
\Rightarrow &A_{Kreis} = 176,7 cm^2 \\
\\
O_{ges} &= M_{DFN} – M_{EFM} + A_{Kreis} \\
&= 223,8 – 35,8 + 176,7 \\
\Rightarrow &O_{ges} = 364,7 cm^2 \end{align}
