2.0 Die Parabel \( p_1 \) verläuft durch die Punkte \( P(2| 6) \) und \(Q(8|3)\) . Sie hat eine Gleichung der Form \( y = ax^2 + bx + 3 \) und \( a \in \mathbb{R} \) \ \( 0 \text{ und } G = \mathbb{R} x \mathbb{R} \) .
Die Parabel \( p_2 \) besitzt die Gleichung \( y = \frac{1}{8} x² – \frac{1}{2} x – 2 \) mit \( G = \mathbb{R} x \mathbb{R} \) .
2.1 Zeigen Sie durch Berechnung der Werte für a und b, dass die Parabel \( p_1 \) die Gleichung \( y = – 0,25x² + 2x + 3\) besitzt.
Lösung zu 2.1
Es sind zwei Punkte P und Q gegeben, also arbeitest du mit einem Gleichungssystem
\begin{align} &\text{P in p:}\\
(1) y &= ax² + bx + 3 \\
6 &= a \cdot 2^2 + b \cdot 2 + 3 \\
6 &= 4a + 2b + 3 \,\,\, |-3 \\
3 &= 4a + 2b \\
\\
&\text{Q in p:}\\
(2) y &= ax² + bx + 3 \\
3 &= a \cdot 8^2 + b \cdot 8 + 3 \,\,\, |-3 \\
0 &= 64a + 8b \\
\\
GTR &=\Rightarrow a = -0,25 \, ; \, b = 2 \\
&\Rightarrow y = -0,25x² + 2x + 3 \end{align}
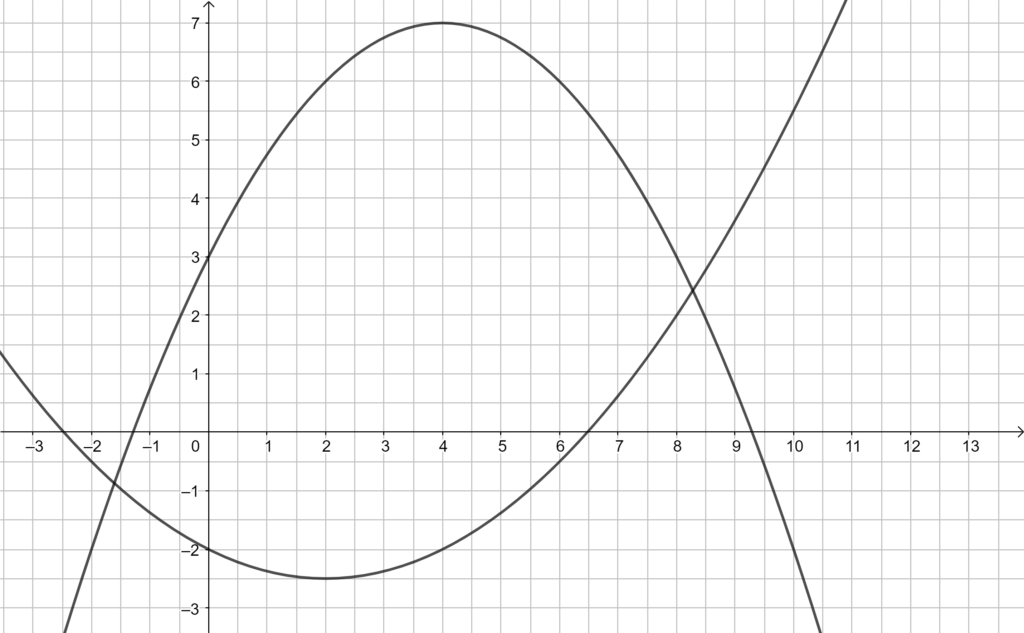
2.2 Zeichnen Sie sodann die Parabel p1 und p2 für x ∈ [– 2 ; 9] in ein Koordinatensystem.
Für die Zeichnung: Längeneinheit 1cm; x ∈ [– 3; 10] ; y ∈ [– 3 ; 8].
Lösung zu 2.2
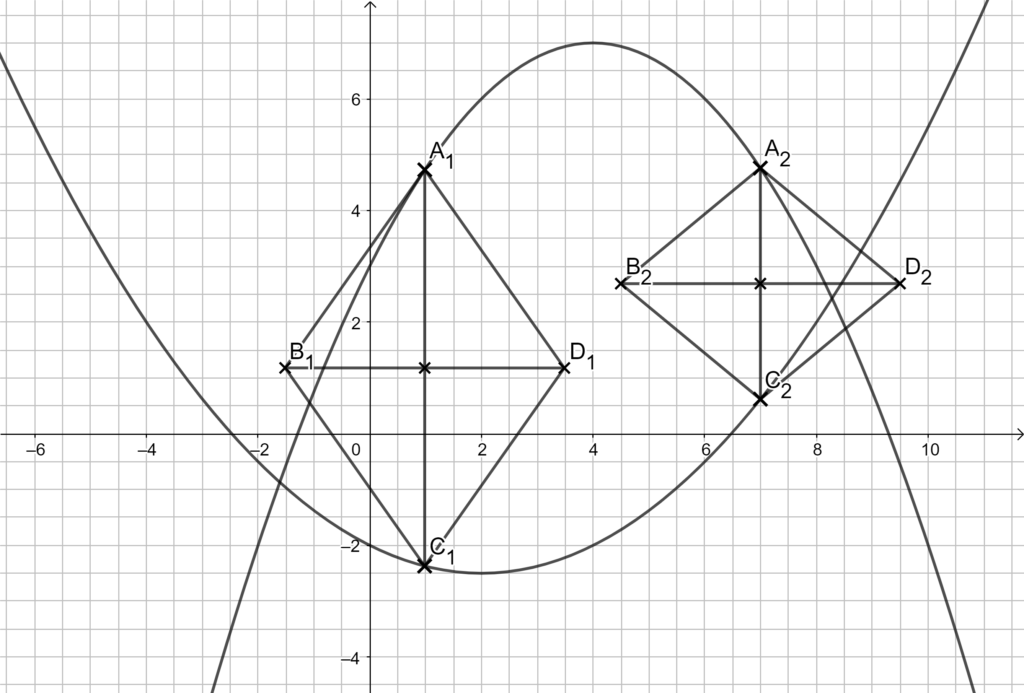
2.3 Punkte \( A_n (x| – 0,25x² + 2x + 3) \) auf der Parabel p1 und Punkte \( C_n(x | \frac{1}{8}x² – \frac{1}{2} x – 2)\) auf der Parabel p2 haben dieselbe Abszisse x. Sie sind zusammen mit Punkten Bn und Dn für x ∈ ] – 1,61; 8,28[ Eckpunkte von Rauten AnBnCnDn mit den Diagonalenschittpunkten Mn.
Für die Länge der Diagonalen \( |\overline{B_n D_n}|\) gilt: \( |\overline{B_n D_n}|\) = 5 LE.
Zeichnen Sie Rauten A1B1C1D1 für x = 1 und A2B2C2D2 für x = 7 in das Koordinatensystem zu 1.1 ein.
Lösung zu 2.3
2.4 Bestimmen Sie das Intervall für x, für welches Rauten ABCD existieren.
Runden Sie ab sofort auf zwei Stellen nach dem Komma.
Lösung zu 2.4
Um die Schnittpunkte zu berechnen, setzt du die Parabelterme gleich und löst die Gleichung mit deinem Taschenrechner.
\begin{align}
y_{p_1} &= y_ {p_2} \\
-0,25x² + 2x + 3 &= 0,125x² – 0,5x – 2 \,\,\, |-0,125x² + 0,5x + 2 \\
-0,375x² +2,5x + 5 &= 0 \\
&\Rightarrow Taschenrechner: x_1 = 8,28 \, ; \, x_2 = -1,61 \\
&\Rightarrow x \in ]-1,61 ; 8,28[ \end{align}
2.5 Zeigen Sie durch Rechnung, dass für den Flächeninhalt A(x) der Rauten gilt:
A(x) = ( – 0,94x² + 6,25x + 12,5) FE
Lösung zu 2.5
Den Flächeninhalt einer Raute bestimmst du mit der Formel \(A = 0,5 \cdot e \cdot f \).
Die Diagonalen sind hier \( |\overline{A_n C_n}| \) und \(|\overline{Bn Dn}|\).
Laut Angabe gilt \(|\overline{Bn Dn} = 5 \) und weil A und C dieselbe Abszisse x haben, kannst du die Streckenlänge durch „Oben – unten“ bestimmen.
\begin{align} &|\overline{An Cn}| \text{ durch „oben – unten“:}\\
|\overline{An Cn} (x)| &= y_A – y_c \\
&= -0,25x² + 2x + 3 – (0,125x² – 0,5x – 2) \\
&= -0,25x² + 2x + 3 – 0,125x² + 0,5x + 2 \\
\Rightarrow &|\overline{A_n C_n}(x)| = -0,375x² +2,5x + 5 \\
\\
&\text{ Berechnung der Rautenfläche über die Flächenformel}\\
A(x) &= 0,5 \cdot |\overline{A_n C_n}| \cdot |\overline{Bn Dn}| \\
&= 0,5 \cdot (-0,375x² +2,5x + 5) \cdot 5 \\
&= 2,5 \cdot (-0,375x² +2,5x + 5) \\
&\Rightarrow A(x) = (- 0,9375x² + 6,25x + 12,5) FE \\
&= \text{ gerundet: } A(x) = (-0,94x² + 6,25x + 12,5) FE \end{align}
2.6 Bestimmen Sie den Wert für x, für den sich Quadrate A3B3C3D3 und A4B4C4D4 ergeben.
Lösung zu 2.6
Eine Raute ist genau dann ein Quadrat, wenn die Diagonalen gleiche Länge haben. Mit dieser Info lässt sich eine Gleichung aufstellen und lösen.
\begin{align}
|\overline{A_n C_n}| &= |\overline{Bn Dn}| \\
-0,375x² +2,5x + 5 &= 5 \,\,\, |-5 \\
-0,375x² +2,5x &= 0 \\
&\Rightarrow Taschenrechner x_1 = 6,67 ; x_2 = 0
\end{align}
Für 6,67 und 0 sind die Rauten gleichzeitig Quadrate.
2.7 Begründen Sie rechnerisch, dass für das Maß der Winkel AnDnMn gilt:
AnDnMn < 65°.
Lösung zu 2.7
Der Winkel \( \angle An Dn Mn \) hat sein größtes Maß, wenn die Diagonale [A_n C_n] ihre maximale Länge erreicht.
Du kannst die längste Diagonale mit deinem Taschenrechenr bestimmen: x = 3,33 mit \( |\overline{A_0 C_0}| \) = 9,17.
Im Dreieck AMD mit der halben Diagonale [AM] kannst du mit dem Tangens diesen größten Winkel ausrechnen.
\begin{align} \\
tan{angle A_0 D_0 M_0 } &= \frac{|\overline{AM}|}{|\overline{MD}|} \\
&= \frac{4,59}{2,5} \,\,\, |tan^{-1}\\
&\Rightarrow \angle A_0 D_0 M_0 = 61,42° \end{align}
Der größte auftretende Winkel ist 61,42°, also kleiner als 65°.
