1.0 Der Punkt S(1|3) ist der Scheitelpunkt der Parabel p mit einer Gleichung der Form
y = – 0,4x² + bx + c mit G = ℝ x ℝ und b,c ∈ ℝ.
Die Gerade g hat die Gleichung y = 0,2x + 6 mit G = ℝ x ℝ.
1.1 Zeigen Sie durch Berechnung der Werte für b und c, dass die Parabel die Gleichung y = – 0,4x²+ 0,8x + 2,6 hat.
Lösungen zu 1.1
\begin{align} &\text{Einsetzen in die Scheitelform:}\\
y &= a \cdot (x – x_S)^2 + y_S \,\,\, \text{ mit a = -0,4 und S(1|3)}\\
&= -0,4 \cdot (x – 1)^2 +3 \\
&= -0,4 \cdot (x² -2x + 1) + 3 \\
&= -0,4x² + 0,8x + 2,6 \end{align}
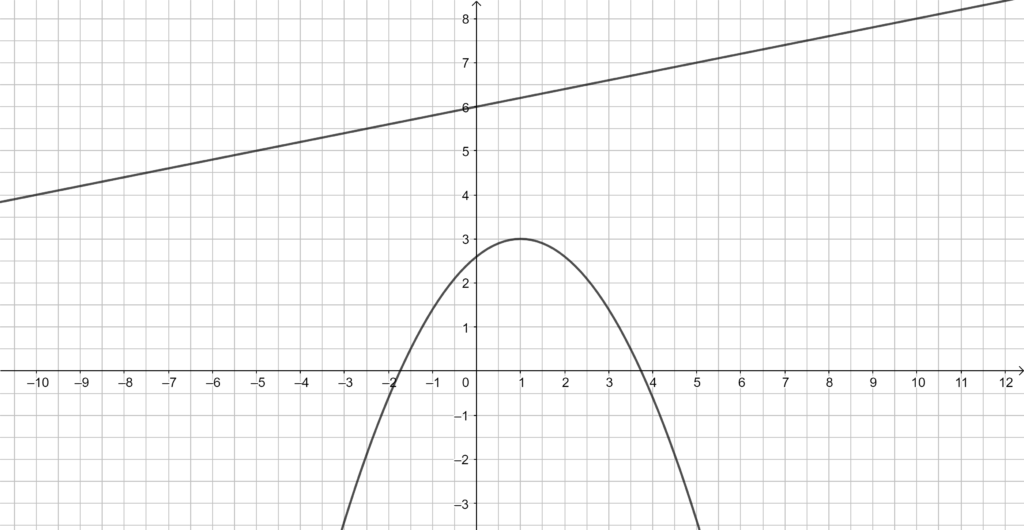
1.2 Zeichnen Sie die Parabel p für x ∈ [–3 ; 5] und die Gerade g in ein Koordinatensystem.
Für die Zeichnung: Längeneinheit 1 cm; x ∈ [-6 ; 6] ; y ∈ [-4 ; 8]
Lösung zu 1.2
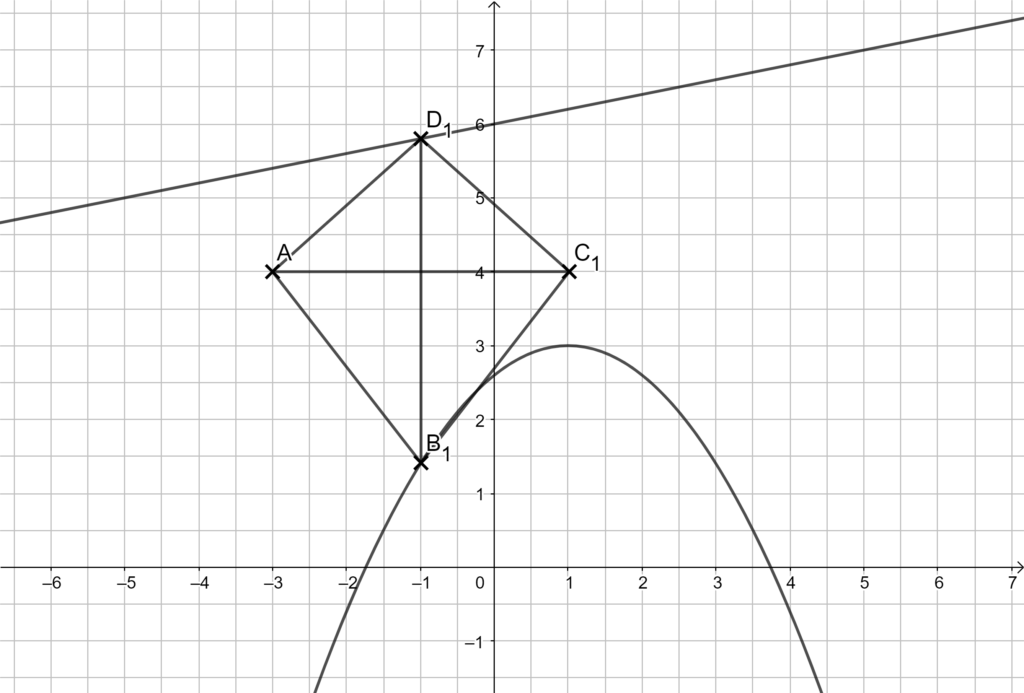
1.3 Punkte Bn (x | – 0,4x² + 0,8x + 2,6) auf der Parabel p und Punkte Dn (x | 0,2x + 6) auf der Geraden g haben dieselbe Abszisse x und bilden zusammen mit den Punkten A(– 3|4) und Punkten Cn Drachenvierecke ABnCnDn.
Zeichnen Sie das Drachenviereck AB1C1D1 für x = – 1 ins Koordinatensystem zu 2.1 ein.
Lösung zu 1.3
1.4 Geben Sie alle Werte x an, für welches Drachenvierecke ABnCnDn existieren.
Lösung zu 1.4
Die Gerade un die Parabel haben keine Schnittpunkte. Du kannst also keine Schnittpunkte der Funktionen bestimmen.
Hier kommt das Problem mit den Bezeichnungen ins Spiel. Liegt die Diiagonale BD rechts vom Punkt A, dann heißt das Viereck ABCD.
Liegt die Diagonale aber links von A, dann spiegelt es den Punkt C auf die andere Seite und das Viereck heißt ADCB, was nicht erlaubt ist.
Die Diagonale muss also rechts von A liegen und es gilt: x > -3 .
1.5 Zeigen Sie rechnerisch, dass für die Strecke \(|\overline{B_n D_n}|\) gilt:
\(|\overline{B_n D_n}|\) = (0,4x² – 0,6x + 3,4) LE
Lösung zu 1.5
\begin{align} |\overline{B_n D_n}| &= y_{Gerade} – y_{Parabel} \\
&= 0,2x + 6 – (-0,4x² +0,8x + 2,6) \\
&= 0,2x + 6 + 0,4x² – 0,8x – 2,6\\
&\Rightarrow |\overline{B_n D_n}| = (0,4x² – 0,6x + 3,4) LE \end{align}
1.6 Bestimmen Sie die Werte für x, für die die Diagonalen des Drachenvierecks gleich lang sind.
(Ersatzergebnis: \(|\overline{AC_n}|\) = (2x + 6) LE )
Lösung zu 1.6
Um die Aufgabe zu lösen, setzen wir die Diagonalenlängen gleich und lösen die Gleichung. Die Diagonale \(|\overline{B_n D_n}|\) kennst du aus 2.5, bleibt \(|\overline{A C_n}|\) zu bestimmen.
Weil A die x-Koordinate -3 hat und die andere Diagonale bei x liegt, ist der Abstand von A zu \(|\overline{B_n D_n}|\) immer x + 3.
Die volle Diagonale ist dann das Doppelte: \( |\overline{AC_n}|= 2x + 6 \) .
\begin{align} |\overline{B_n D_n}| &= |\overline{AC_n}| \\
0,4x² – 0,6x + 3,4 &= 2x + 6 \,\,\, |-2x – 6 \\
0,4x² – 2,6x – 2,6 &= 0 \\
&\Rightarrow \text{Taschenrechner:} \, x_1 = 7,38 \, ; \, x_2 = -0,88 \end{align}
1.7 Bestimmen Sie die Werte für x, für die gilt: Winkel ∢ ADC = 90°.
Lösung zu 1.7
Diese Aufgabe lässt sich auch mit Sinus, Cosinus und Tangens lösen, aber ich möchte einen Lösungsweg ohne Triggonometrie zeigen. Zuerst benennen wir den Schnittpunkt der Diagonalen: Ich nenne ihn M.
Dass bei D ein rechter Winkel entsteht, muss der Winkel \( \angle ADM \) = 45° sein. Das liegt an der Symmetrie des Drachenvierecks, da sich der 90° Winkel gleich aufteilt. Damit bleibt für den Winkel \( \angle DAM \) noch 45° übrig, denn die Innenwinkelsumme muss ja 180° ergeben.
Das Dreieck AMD ist in diesem Fall also gleichschenklig mit den Schenkeln \( \overline{AM} \text{und} \overline{MD}\). Damit lässt sich eine Gleichung aufstellen:
\begin{align} &|\overline{AM}| = |\overline{MD}| \\
|\overline{AC}|/2 &= y_D – y_A \\
(2x + 6)/2 &= 0,2x + 6 – 4 \\
x + 3 &= 0,2x + 2 \,\,\, |-0,2x – 3 \\
0,8x &= -1 \,\,\, |:0,8 \\
x &= – 1,25 \end{align}
Für x = – 1,25 ist die vorgegebene Eigenschaft erfüllt.
