

Lösung zu B4.1
AC soll die Schrägbildachse sein. Du musst von M also nach vorne und nach hinten!
Für die Berechnungen suchst du dir ein rechtwinkliges Dreieck. Wie war das nochmal mit der Höhe?
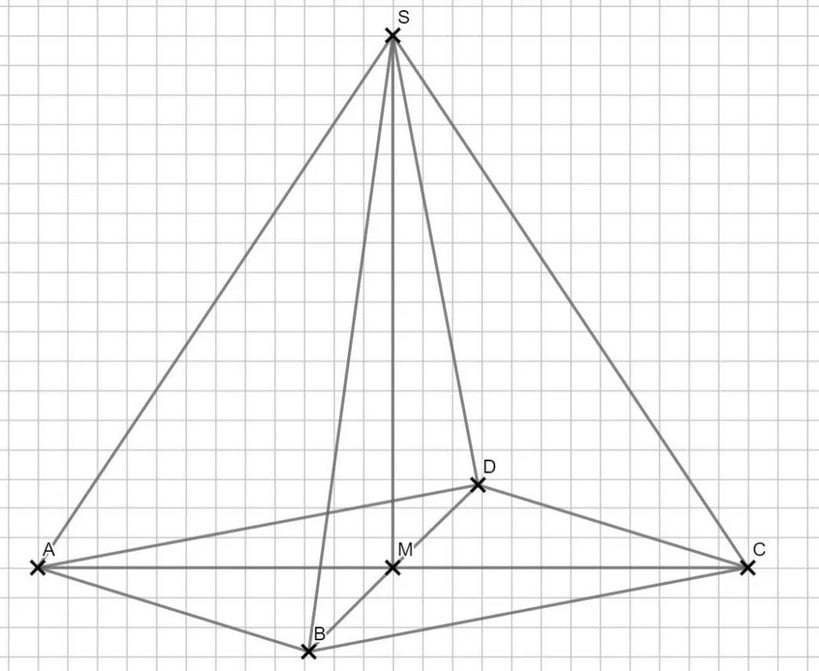
\begin{align} &|\overline{AS}| \text{ mit dem Satz des Pythagoras:}\\
|\overline{AS}|^2 &= |\overline{AM}|^2 + |\overline{MS}|^2 \\
&= 6^2 + 9^2 \,\,\, |\sqrt{}\\
\Rightarrow &|\overline{AS}| = 10,82 cm \\
\\
&\angle CAS \text{ mit dem Tangens:}\\
tan(\angle CAS) &= \frac{ |\overline{MS}| } {|\overline{AM}|} \\
&= \frac{9}{6}\,\,\, |tan^{-1}\\
\Rightarrow &\angle CAS = 56,31° \end{align}

Lösung zu B4.2
Starte beim Lesen mit der Angabe für x, also 5. Wo liegt P? Welche Punkte musst du mit P verbinden.
Bevor du das Volumen berechnest, schaue in die Zwischenergebnisse. Diese sind der Weg zum Ziel.
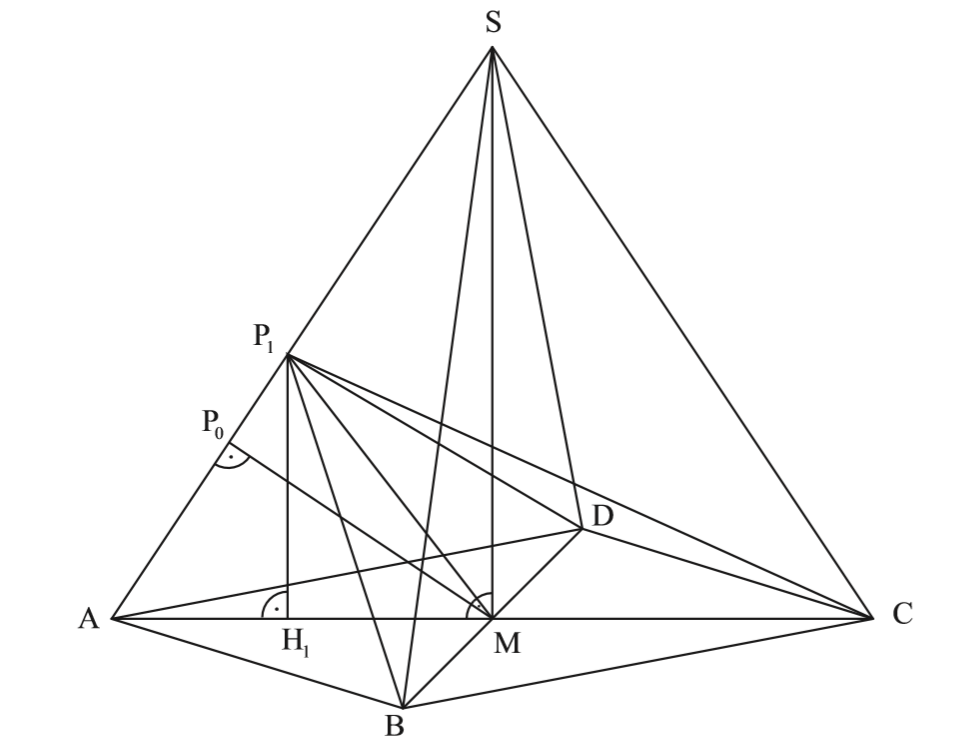
\begin{align} &|\overline{MP_1}| \text{ mit dem Cosinussatz im Dreieck } AMP_1: \\
|\overline{MP_1}|^2 &= |\overline{AM}|^2 + |\overline{AP_1}|^2 – 2 \cdot |\overline{AM}| \cdot |\overline{AP_1}| \cdot cos(\angle CAS)\\
&= 6^2 + 5^2 – 2 \cdot 6 \cdot 5 \cdot cos(56,31°)\,\,\, |\sqrt{}\\
\Rightarrow &|\overline{MP_1}| = 5,26 cm \\
\\
&|\overline{H_1 P_1}| \text{ mit dem Sinus im Dreieck } AH_1 P_1: \\
sin(\angle CAS) &= \frac{ |\overline{H_1 P_1}| } { |\overline{AP_1}|}\\
sin(56,31°) &= \frac{ |\overline{H_1 P_1}| } {5} \,\,\, |\cdot 5 \\
\Rightarrow &|\overline{H_1 P_1}| = 4,16 cm \\
\\
&V \text{ mit der Volumenformel:}\\
V &= \frac{1}{3} \cdot \,\, 0,5 \cdot |\overline{BD}| \cdot |\overline{AM}| \,\, \cdot |\overline{H_1 P_1}|\\
&= \frac{1}{3} \cdot 0,5 \cdot 8 \cdot 6 \cdot 4,16 \\
\Rightarrow &V = 33,28 cm^3 \end{align}

Lösung zu B4.3
Anstatt den Flächeninhalt direkt zu berechnen, kannst du ein größeres Dreieck nehmen und etwas davon abziehen.
Hier gibt es viele Lösungswege. Du könnest z.B. den Winkel bei S berechnen und dann mit der Sinusformel arbeiten.
Ich zeige hier die Lösung, die aus dem Tipp folgt. Man berechnet den Flächeninhalt des Dreiecks AMS und zieht dann den Flächeninhalt von AMP1 ab. Ich finde diesen Weg besser, weil man schon alle Strecken kennt und keine Zwischenschritte braucht.
\begin{align}
A_{MSP_1} &= A_{AMS} &-& A_{AMP_1} \\
&= 0,5 \cdot |\overline{AM}| \cdot |\overline{MS}| &-&0,5 \cdot |\overline{AM}| \cdot |\overline{H_1 P_1}|\\
&= 0,5 \cdot 6 \cdot 9 &- &0,5 \cdot 6 \cdot 4,16 \\
\Rightarrow &A_{MSP_1} = 14,52 cm² \end{align}

Lösung zu B4.4
Schau mal in B4.2. Da ist P0 schon eingezeichnet. Hier findest du auch den Tipp, wie man diesen Punkt findet.
Rechne für die Begründung den Flächeninhalt von BDP0 aus und überlege dir, was dieses Ergebnis bedeutet.
Weil für P0 die kürzeste Strecke ist, hat BDP0 den kleinsten Flächeninhalt. Ist dieser Flächeninhalt größer als 18, kann es kein Dreieck mit 18 cm² geben. Bleibt auszurechnen, wie groß der Flächeninhalt nun wirklich ist.
Bei P0 entsteht ein rechter Winkel, weshalb du Sin, Cos, Tan verwenden darfst.
\begin{align} &|\overline{MP_0} \text{ mit dem Sinus im Dreieck }AMP_0:\\
sin(\angle CAS) &= \frac{|\overline{MP_0}| }{|\overline{AM}|} \\
sin(56,31°) &= \frac{|\overline{MP_0}|}{6} \,\,\, |\cdot 6 \\
\Rightarrow &|\overline{MP_0}| = 4,99 cm\\
\\
&A \text{ mit der Flächenformel:}\\
A &= 0,5 \cdot |\overline{BD}| \cdot |\overline{MP_0}|\\
&= 0,5 \cdot 8 \cdot 4,99 \\
\Rightarrow &A = 19,96 cm² \end{align}
Das kleinste Dreieck hat eine Fläche von 19,96 cm². Es gibt keine kleineren Dreiecke. Also auch keines mit 18 cm²
