

Lösung zu B3.1
Ist der Scheitelpunkt gegeben, musst du in die Scheitelform einsetzen. Hast du zwei Punkte gegeben, brauchst du ein Gleichungssystem. Welcher Fall liegt vor?
Setze den Scheitelpunkt in die Scheitelform ein und vereinfache anschließend.
\( \begin{align} y &= a \cdot ( x – x_S)^2 + y_s \\ \\ &mit \,S(5|-4,5) \\ &und \,a = 0,1 \\ \\y &= 0,1 (x-5)^2 -4,5 \\ &= 0,1 \cdot (x^2 -10x +25) -4,5 \\ &= 0,1x^2 -x + 2,5 – 4,5 \\ \Rightarrow &y = 0,1x^2 -x -2 \end{align} \)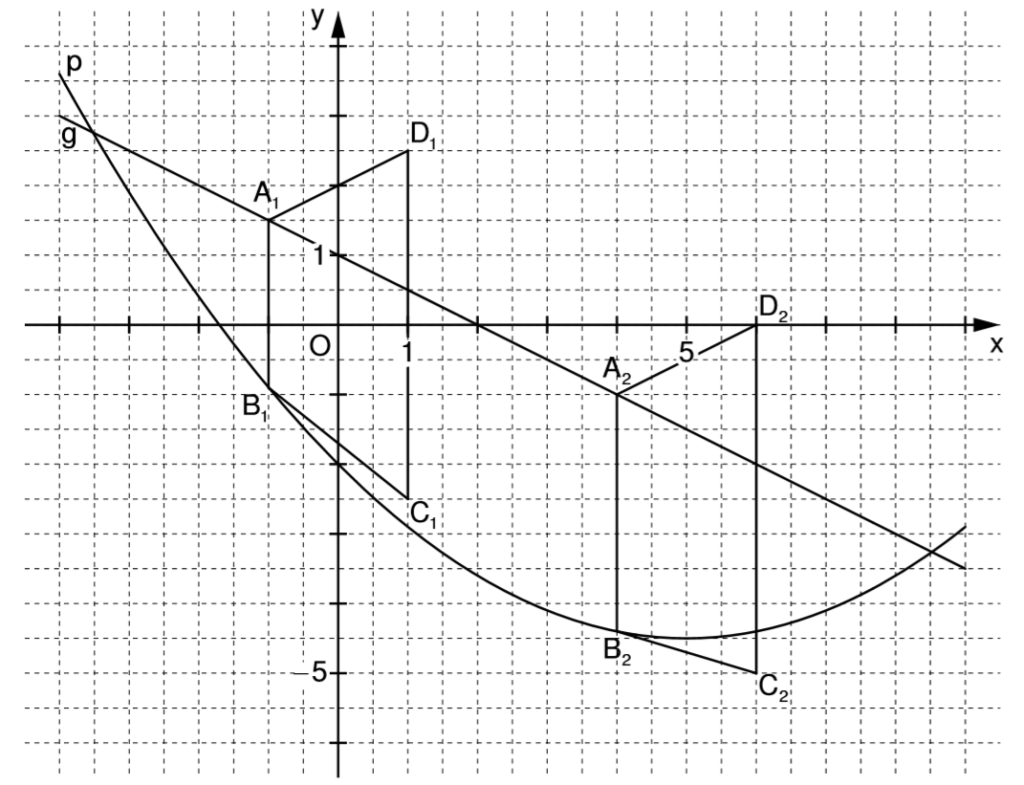
Das Video ist zwar vom Haupttermin 2020, aber die Aufgabenstellung ist mit der Musterlösung identisch. Hier ist also wirklich die Lösung erklärt.
Zurück zum MAP-Hack:

Lösung zu B3.2
Gehe zuerst zum angebenen x-Wert – also -1 – und zeichne A und B ein. Der Vektor sagt dir, wie du von A zu D kommst. Oben steht die x-Koordinate, unten die y-Koordinate.
Die eingezeichneten Trapeze findest du in B3.1
Das Video ist zwar vom Haupttermin 2020, aber die Aufgabenstellung ist mit der Musterlösung identisch. Hier ist also wirklich die Lösung erklärt.
Zurück zum MAP-Hack:

Lösung zu B3.3
Setze die Funktionsterme gleich und löse nach „= 0“ auf.
Berechne die Nullstellen mit deinem Taschenrechner:
\begin{align} \Rightarrow GTR: \, x_1 &= 8,52 \, x_2 = -3,52 \\ x & \in ]-3,52 ; 8,52[ \end{align}
Das Video ist zwar vom Haupttermin 2020, aber die Aufgabenstellung ist mit der Musterlösung identisch. Hier ist also wirklich die Lösung erklärt.
Zurück zum MAP-Hack:

Lösung zu B3.4
Um in die Flächenformel für das Trapez einsetzen zu können, benötigst du die Länge der Strecke [AB]. Weil A und B dieselbe Abszisse haben, kannst du „oben – unten“ rechnen.
Das Video ist zwar vom Haupttermin 2020, aber die Aufgabenstellung ist mit der Musterlösung identisch. Hier ist also wirklich die Lösung erklärt.
Zurück zum MAP-Hack:

Lösung zu B3.5
Überlege dir, welche Streckenlängen sich nicht verändern und was das mit AB zu tun hat. Fasse deine Gedanken in Worte und schreibe sie als Antwort auf.
Die Erklärung zu den 3 LE gibt es im Video 🙂
\( \begin{align} &\angle D_4 C_4 B_4 \text{ mit dem Tangens:} \\ tan(\angle D_4 C_4 B_4 ) &= \frac{2}{1} \\ \Rightarrow \angle D_4 C_4 B_4 &= 63,43° \end{align} \)