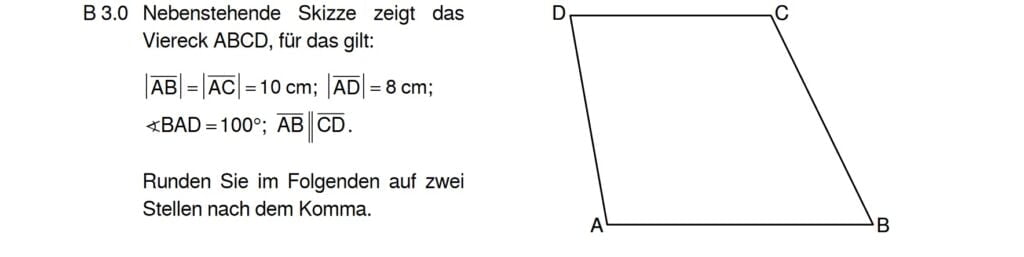

Lösung zu 3.1
Im rechtwinkligen Dreieck hast du Sin/Cos/Tan und SdP zur Auswahl. Gibt es keinen rechten Winkel, bleibt nur noch Sinussatz und Cosinussatz.
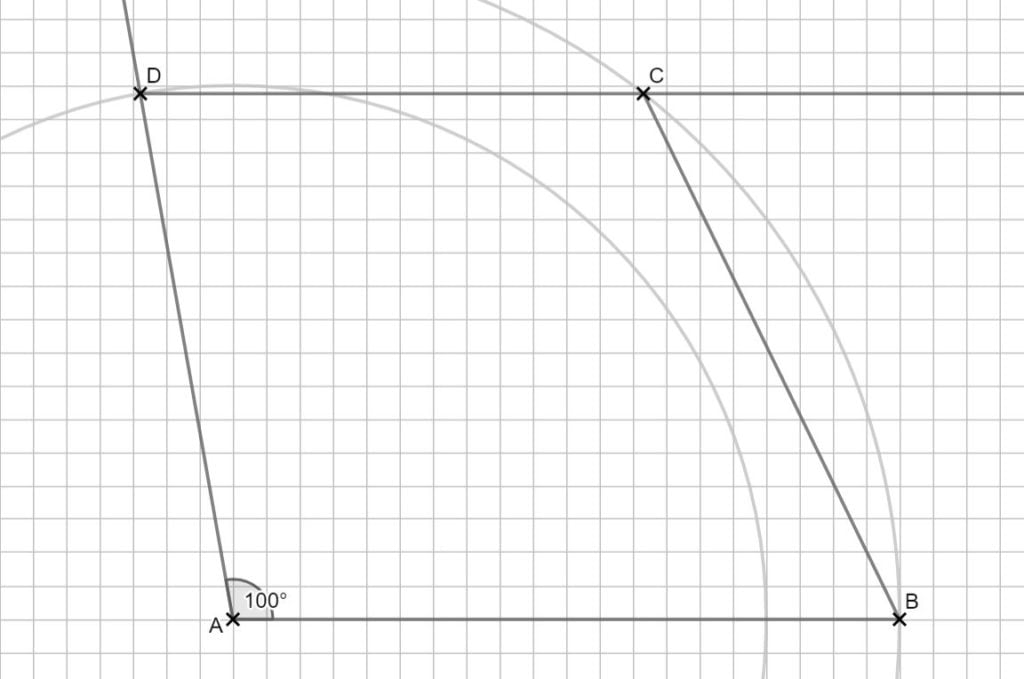
Achtung, nicht wie ich die Diagonalen vergessen 😉
\begin{align} & |\overline{BD}| \text{ mit dem Cosinus-Satz:} \\
|\overline{BD}|^2 &= |\overline{AB}|^2 +| \overline{AD}|^2 – 2 \cdot |\overline{AB}| \cdot |\overline{AD}| \cdot cos(\angle BAD) \\
&= 10^2 + 8^2 – 2 \cdot 10 \cdot 8 \cdot cos(100°) \\
\Rightarrow & |\overline{BD}| = 13,85 cm \\
\\
& \angle DBA \text{ mit Sinus-Satz:} \\
\frac{sin(\angle DBA)}{|\overline{AD}|} &= \frac{sin(\angle BAD)}{|\overline{BD}|} \\
\\
\frac{sin(\angle DBA)}{8} &= \frac{sin(100°)}{13,85} \, \, | \cdot 8 \\
sin(\angle DBA) &= \frac{sin(100°)}{13,85} \cdot 8 \\
\Rightarrow \angle DBA &= 34,67° \end{align}
Zurück zum MAP-Hack:

Lösung zu 3.2
Zeit für besondere Winkelbeziehungen – Stoff der 7. Klasse. Wechsel-, Stufen- oder Ergänzungswinkel. Was war das denn nochmal?
\begin{align} & \angle DCA \text{ mit dem Sinussatz:} \\
\frac{sin(\angle DCA)}{|\overline{AD}|} &= \frac{sin(180° – 100°)}{|\overline{AC}|} \\
\frac{sin(\angle DCA)}{8} &= \frac{sin(80°)}{10} \, \, |\cdot 8 \\
sin(\angle DCA) &= \frac{sin(80°)}{10} \cdot 8 \\
\Rightarrow &\angle DCA = 51,98° \end{align}
Weil AB und CD parallel zueinander sind, sind die Winkel BAC und DCA Wechselwinkel und deshalb gleich groß. In mathematischen Bezeichnungen:
\( AB || CD \Rightarrow \angle BAC = \angle DCA = 51,98° (\text{Wechselwinkel}) \)
Lösung zu 3.3
Das Viereck setzt sich aus den Dreiecken △ABC und △ACD zusammen. Du berechnest die Flächeninhalte der einzelnen Dreiecke und addierst anschließend.
Das Viereck setzt sich aus den Dreiecken \(\triangle ABC \) und \(\triangle ACD \) zusammen. Du berechnest die Flächeninhalte der einzelnen Dreiecke und addierst anschließend.
\begin{align} A_{\triangle ABC} &= 0,5 \cdot |\overline{AB}| \cdot |\overline{AC}| \cdot sin(\angle BAC) \\
&= 0,5 \cdot 10 \cdot 10 \cdot sin(51,98°) \\
\Rightarrow &A_{\triangle ABC} = 39,39 cm^2 \\
\\
A_{\triangle ACD} &= 0,5 \cdot |\overline{AC}| \cdot |\overline{AD}| \cdot sin(\angle CAD) \\
&\angle CAD = \angle BAD – \angle BAC = 100° – 51,98° \\
& \Rightarrow \angle CAD = 48,02° \\
A_{\triangle ACD} &= 0,5 \cdot 10 \cdot 8 \cdot sin(48,02°) \\
\Rightarrow &A_{\triangle ACD} = 29,74 cm^2 \\
\\
A_{ABCD} &= A_{\triangle ABC} + A_{\triangle ACD} \\
&= 39,39 + 29,74 \\
\Rightarrow &A_{ABCD} = 69,13 cm^2 \end{align}
Zurück zum MAP-Hack:

Lösung zu 3.4
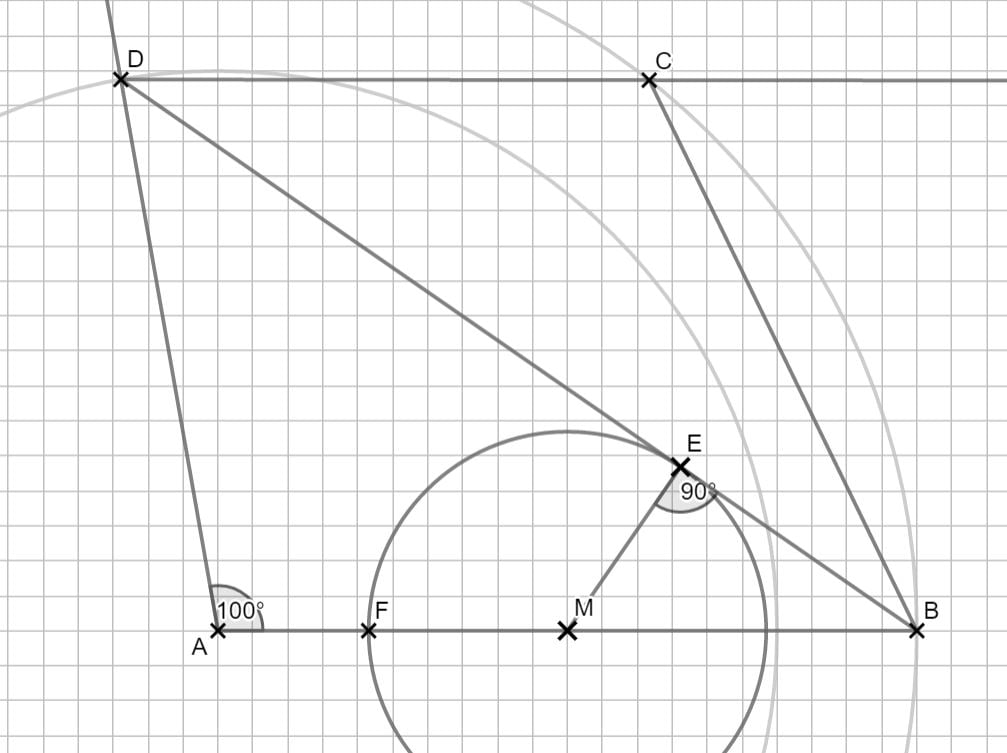
Im Berührpunkt steht der Radius senkrecht auf die Strecke. So findest du den Punkt E mit deinem Geodreieck.

Zurück zum MAP-Hack:

Lösung zu 3.5
Die gesuchte Fläche setzt sich aus den Flächen des Kreissektors, der durch E und F begrenzt ist, und dem Dreieck BEM zusammen. Weil der Kreis in E die Strecke berührt, ist dort ein rechter Winkel.
Die gesuchte Fläche setzt sich aus den Flächen des Kreissektors, der durch E und F begrenzt ist, und dem Dreieck BEM zusammen. Weil der Kreis in E die Strecke berührt, ist dort ein rechter Winkel.
Um den Flächeninhalt des Dreiecks zu berechnen benötigst du die Länge der Strecke ME:
\begin{align} &A_{\triangle BEM} \text{ über} |\overline{ME}|: \\
sin(\angle EBM) &= \frac{|\overline{ME}|}{|\overline{BM}|} \, \, |\cdot |\overline{BM}| \\
|\overline{ME}| &= sin(\angle EBM) \cdot |\overline{BM}| \\ &= sin(34,67°) \cdot 5 = 2,84 cm \\
\\
\angle BME &= 180° – \angle MEB – \angle EBM \,\,\, (\text{Innenwinkelsumme}) \\
&= 180° – 90° – 34,67° \\
\Rightarrow & \angle BME = 55,33° \\
\\
A_{\triangle BEM} &= 0,5 \cdot |\overline{MB}| \cdot |\overline{ME}| \cdot sin(\angle BME) \\
&= 0,5 \cdot 5 \cdot 2,84 \cdot sin(55,33°) \\
\Rightarrow &A_{\triangle BEM} = 5,84 cm^2 \end{align}
Um den Flächeninhalt des Kreissektors zu berechnen, benötigst du den Winkel BME:
\begin{align} A_{Sektor} &= \frac{\angle EMF}{360°} \cdot \overline{ME}^2 \cdot \pi \\
\\
\angle EMF &= 180° – \angle BME \,\,\, (\text{Ergänzungswinkel}) \\
&= 180° – 55,33° \\
\Rightarrow \angle EMF &= 124,67° \\
\\
A_{Sektor} &= \frac{124,67°}{360°} \cdot 2,84^2 \cdot \pi \\
\Rightarrow &A_{Sektor} = 8,77 cm^2 \\
A &= A_{\triangle BEM} + A_{Sektor} = 5,84 + 8,77 = 14,61 cm^2 \\
\\
&\text{Berechnung des Prozentsatzes:} \\
p &= \frac{A}{A_{ABCD}} \cdot 100 \% \\ &= \frac{14,61}{69,12} \cdot 100 \% = 21,14 \% \end{align}
Zurück zum MAP-Hack:

Lösung zu 3.6
Grundwissen aktivieren: https://map-hack.de/grundwissen/eigenschaften-des-abstandes/
\begin{align} &\angle CGD \text{ mit der Innenwinkelsumme:} \\ \angle CGD &= 180° – 51,98° – 34,67° = 93,35° \end{align}
Der Abstand d ist die kürzeste Verbindungsstrecke und steht immer senkrecht (90°). Weil der Winkel größer als 90° ist, ist die Länge Strecke DG auch größer als der Abstand.
