Grundwissen: Vierstreckensatz

Der Vierstreckensatz beschreibt seine Funktion bereits im Namen. Er setzt 4 Strecken in einen Zusammenhang, den wir als Gleichung aufschreiben können.

Um den Vierstreckensatz verwenden zu dürfen, müssen folgende Voraussetzungen erfüllt sein.

1. Es gibt zwei Geraden, die die sich scheiden.
2. Es gibt zwei Geraden, die parallel zueinander sind.

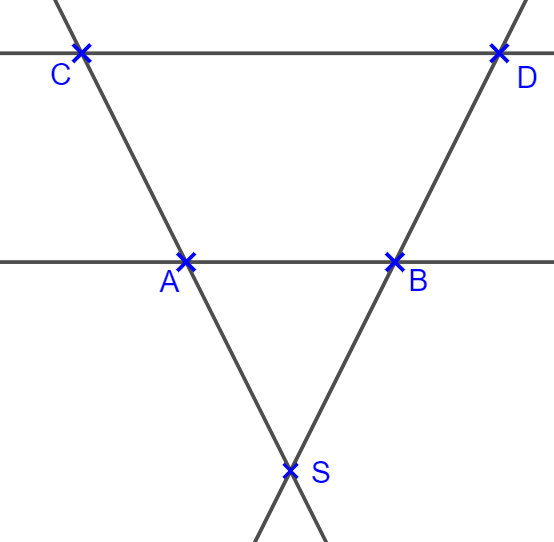
Für die zweite Bedingung gibt es häufig schon das Warnsignal in der Aufgabenstellung. Parallelität muss nämlich explizit in der Aufgabe genannt werden. Hier sollest du besonders auf Schreibweisen  AB || CD (Gerade AB ist parallel zu Gerade CD) achten. Steht diese Angabe in der Aufgabenstellung, kann man häufig den Vierstreckensatz verwenden.

Um die Gleichung aufzustellen, stellen wir uns diese Zeichnung wie zwei Eiswaffeln vor, eine kleine Waffel ASB und eine große Waffel CSB. Dann gilt:

\(\fbox{$ \frac{Kleine\, Waffel}{Kleine\, Waffel} = \frac{Große\, Waffel}{Große\, Waffel}$}\)

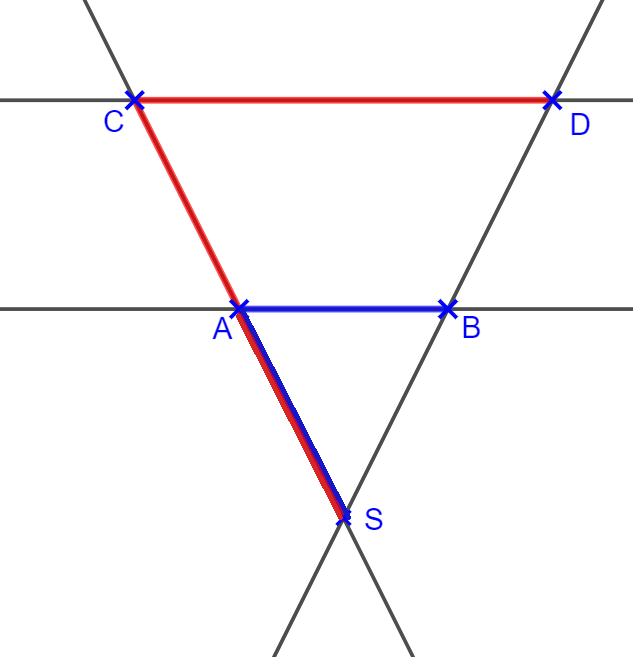
Oder in den math. Bezeichnungen:

\(\fbox{$\frac{|\overline{AB}|}{|\overline{AS}|} =\frac{|\overline{CD}|}{|\overline{CS}|}$} \)

Wenn wir drei Streckenlängen kennen, kann die letzte ausgerechnet werden. Für die Umformung gelten die selben Regeln wir z.B. beim Sinussatz.

Der Vierstreckensatz lässt sich auf sehr viele verschiedene Arten aufstellen. Hier lernst du eine, aber sollte dein Lösungsbuch für MAPs einen anderen Ansatz zeigen, kann er trotzdem stimmen.

Übungsaufgaben zum Vierstreckensatz

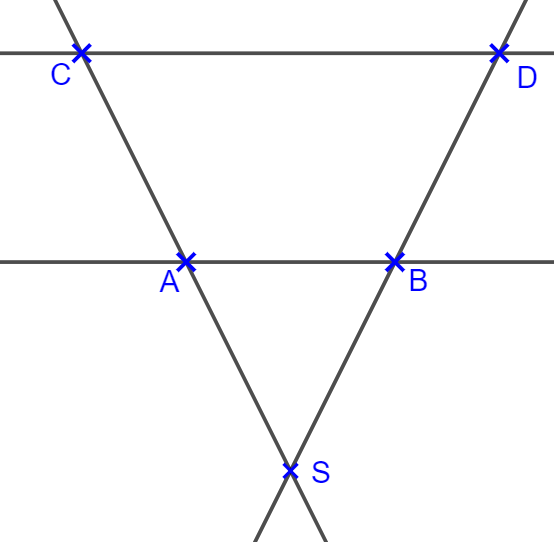
Für folgende Aufgaben gilt die nicht maßstabsgetreue Skizze rechts. Außerdem gilt: AB||CD. Runde Ergebnisse auf zwei Stellen nach dem Komma.

1. \(|\overline{BS}|=3 ; |\overline{DS}|=8 ; |\overline{AB}| = 2. \\ \) Berechne \( |\overline{CD}| \) !
2. \(|\overline{AS}|=2,4 ; |\overline{AC}|=5 ; \overline{AB} = 2. \\ \) Berechne \( |\overline{CD}| \) !