Dreiecke
Rechtwinklige Dreiecke
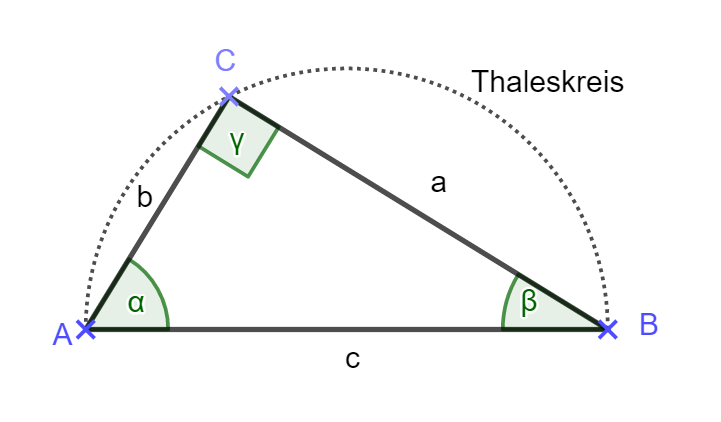
Das rechtwinklige Dreieck hat einen 90° Winkel. Die größte Seite (Hypotenuse) liegt dem rechten Winkel gegenüber. Die anderen beiden Seiten nennt man Katheten.
Werkzeuge: Satz des Pythagoras, Sinus, Cosisnus, Tangens, Innenwinkelsumme im Dreieck, Satz des Thales
Gleischschenklige Dreiecke
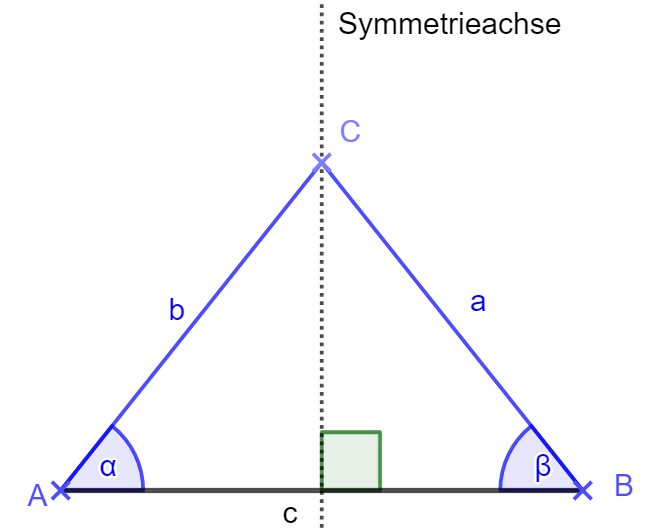
Im gleichschenkligen Dreieck sind zwei Seiten und zwei Winkel gleich groß. Es ist achsensymmetrisch, wobei die Symmetrieachse senkrecht auf einer Seite steht.
Werkezeuge: Sinus-Satz, Cosinus-Satz, im halben Dreieck auch Sin, Cos, Tan, Satz des Pythagoras
Gleichseitige Dreiecke
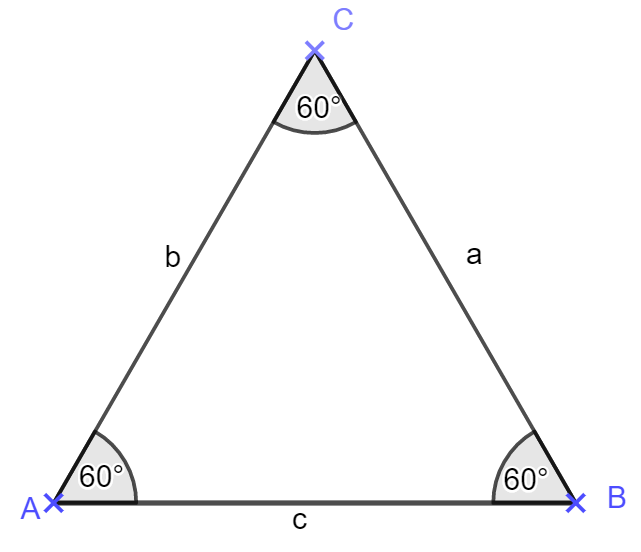
Im gleichseitigen Dreieck sind alle Seiten und alle Winkel gleich groß. Die Winkel haben das Maß 60°
Werkzeuge: Sinus-Satz, Cosinus-Satz
Vierecke
Drachenvierecke
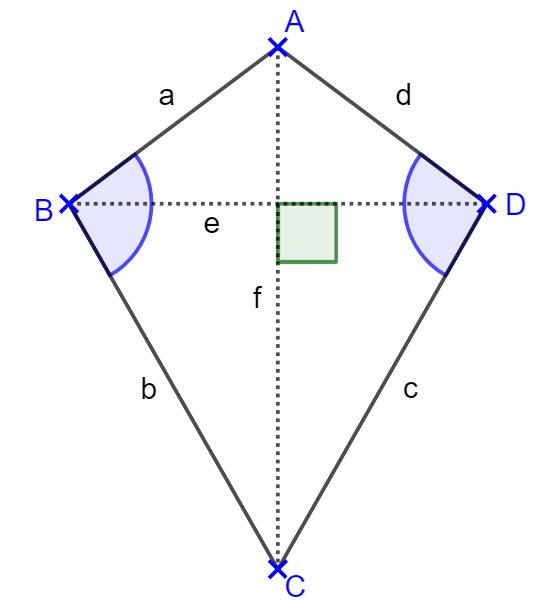
- Es gibt zwei Paare benachbarter Seiten mit selber Länge.
- Die Diagonalen schneiden sich im rechten Winkel.
- Die zwei Winkel zwischen unterschiedlich-langen Seiten haben das selbe Maß.
- Eine Diagonale ist eine Symmetrieachse.
Werkzeuge: Teile das Drachenviereck durch die Diagonalen in Dreiecke und nutze die Eigenschaft, dass diese rechtwinklig sind.
Flächenformel: \( A_{Drache}= \frac {e \cdot f} {2} \)
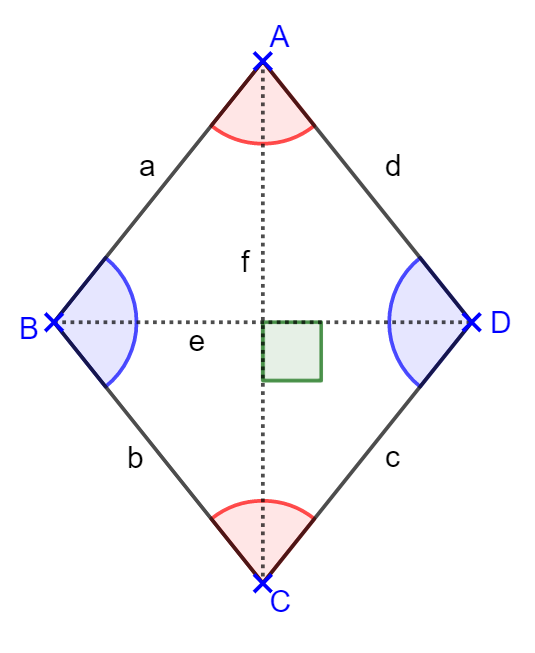
Rauten
- Alle Seiten haben die selbe Länge.
- Gegenüberliegende Winkel haben das selbe Maß.
- Die Diagonalen schneiden sich im rechten Winkel.
- Die Diagonalen halbieren sich.
- Beide Diagonalen sind Symmetrieachsen.
Werkzeuge: Teile die Raute durch die Diagonalen in Dreiecke und nutze die Eigenschaft, dass diese rechtwinklig sind. Halbierst du die Raute, so erhälst du ein gleichschenkliges Dreieck.
Flächenformel: \( A_{Drache}= \frac {e \cdot f}{2} \)
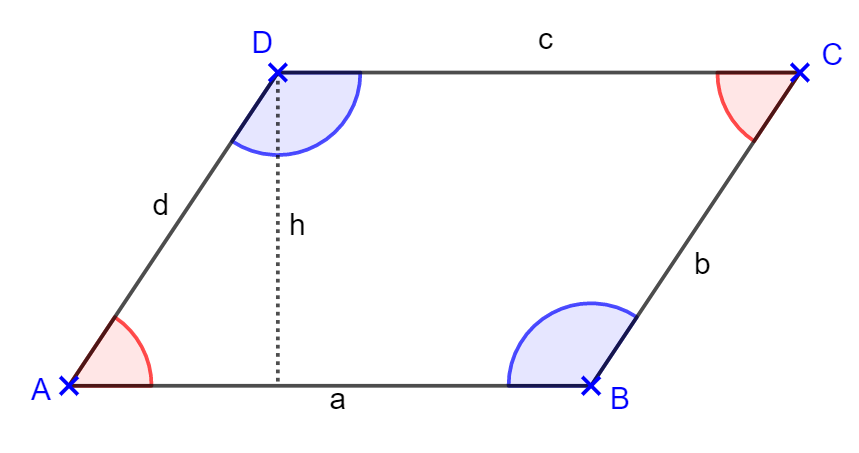
Parallelogramme
- Gegenüberliegende Seiten sind gleich groß.
- Gegenüberliegende Winkel haben das selbe Maß.
- Benachbarte Winkel ergeben 180°.
- Teilt man das Parallelogramm durch eine Diagonale, so stehen zwei kongruente Dreiecke.
Werkzeug: /
Flächenformel: \( A_{Parallellogramm}= g \cdot h\)
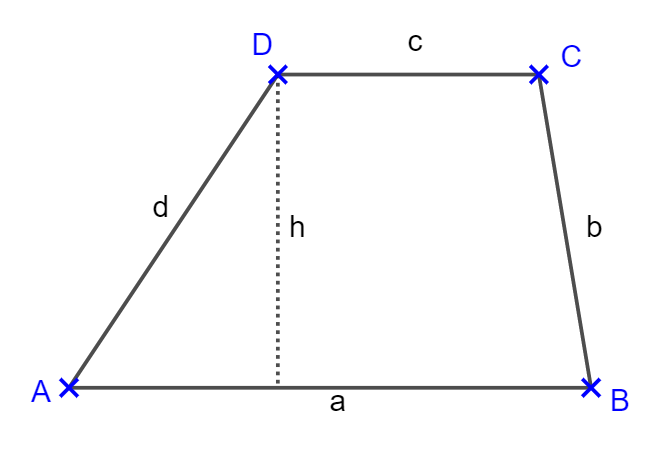
Trapez
Im Trapez sind zwei gegenüberliegende Seiten parallel zueinander. Die Höhe h ist der Abstand dieser Parallelen. Ein Trapez kann einen rechten Winkel haben oder symmetrisch sein.
Werkzeug: /
Flächenformel: \( A_{Trapez} = \frac{(a+c) \cdot h}{2}\)
