4.1
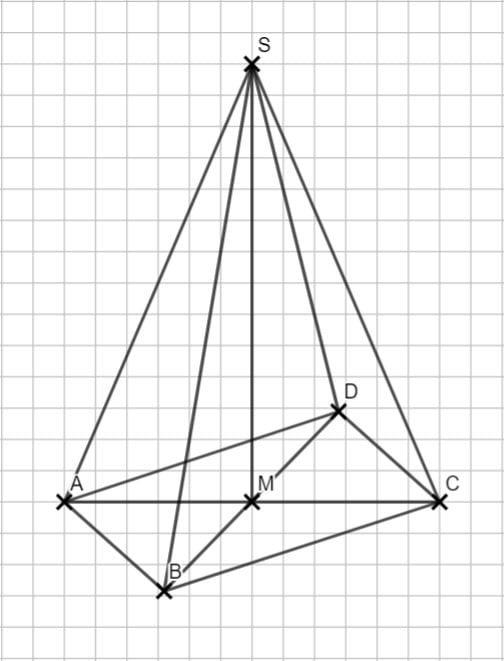
4.2 Alles wie immer! Beim den ersten Berechnungen gibt es auch in der Abschlussprüfung keine Überraschungen.
\begin{align}
|\overline{CS}|^2 &= |\overline{CM}|^2 + |\overline{MS}|^2 \\
&= 3^2 + 7^2 \,\,\, |\sqrt{}\\
&\Rightarrow |\overline{CS}| = 7,6 cm \\
\\
tan(\angle SCM) &= \frac{|\overline{MS}|}{|\overline{CM}|} \\
&= \frac{7}{3} \,\,\, |tan^{-1}\\
&\Rightarrow \angle SCM = 66,8° \end{align}
4.3 Um R zu finden brauchst du deinen Zirkel. Und ja: Es wird unübersichtlich! Ich habe dir das Dreieck für 4.4 in rot markiert.
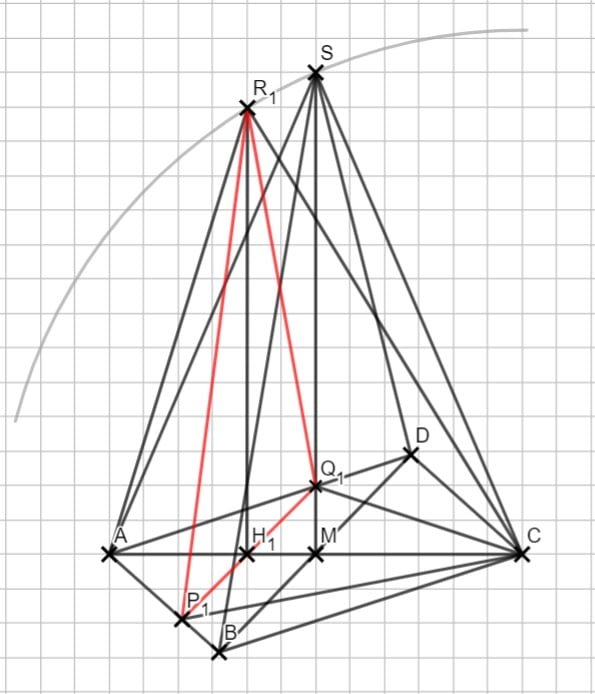
4.4 Ausnahmsweise musst du es nicht in Abhängigkeit von x machen. Es geht um das eingezeichnete Dreieck. Hier bleibt dir also das Rechnen mit x erspart.
\begin{align} \frac{|\overline{P_1 Q_1}|}{|\overline{BD}|} &= \frac{\overline{|A R_1}|}{|\overline{AM}|} \\
\frac{|\overline{P_1 Q_1}|} {8} &= \frac{2}{3} \,\,\, |\cdot 8 \\
|\overline{P_1 Q_1}| &= \frac{2}{3} \cdot 8 \\
&\Rightarrow |\overline{P_1 Q_1}| = 5,3 \\
\\
h &= |\overline{H_1 R_1}| \text{ und } |\overline{CR_n}| = |\overline{CS}| = 7,6 cm\\
|\overline{CR_1}|^2 &= |\overline{H_1 R_1}|^2 + |\overline{CH_1}|^2 \,\,\, |-|\overline{CH_1}|^2 \\
|\overline{CR_1}|^2 -|\overline{CH_1}|^2 &= |\overline{H_1 R_1}|^2 \\
7,6^2 – 4^2 &= |\overline{H_1 R_1}|^2 \,\,\, |\sqrt{} \\
&\Rightarrow |\overline{H_1 R_1}| = 6,5 cm \\
\\
A &= \frac{1}{2} \cdot g \cdot h \\
&= \frac{1}{2} \cdot |\overline{P_n Q_n}| \cdot |\overline{H_n R_n}| \\
&= \frac{1}{2} \cdot 6,5 \cdot 5,3 \\
&\Rightarrow A = 17,2 cm^2 \end{align}
4.5 Nimm dir für diese Aufgaben die Formel und begründe für alles Bestandteile, wie sie sich mit x verändert.
\begin{align} A &= \frac{1}{2} \cdot |\overline{P_n Q_n}| \cdot |\overline{H_n R_n}| \end{align}
Die Grundseite wird größer, je größer das x ist, weil die Strecke weiter von A wegrückt und näher an BD kommt.
Die Höhe wir ebenfalls größer, wenn das x größer wird, da sich der Kreisbogen immer weiter von AC entfernt.
Alle Faktoren werden mit steigendem x größer, also auch der Flächeninhalt.
4.6 Ist die Aufgabe in Abhängigkeit von x nicht beim Flächeninhalt, dann ist sie halt woanders. Zuerst ist dir bestimmt die Wurzel aufgefallen. Diese entsteht als Umkehrung des Quadrats. Welche Formeln kennst du mit Quadraten und du musst Wurzeln ziehen? Der Satz des Pythagoras. Jetzt noch einiges umformen und die komische Aufgabe ist geschafft.
\begin{align} |\overline{C R_n}|^2 &= |\overline{C H_n}|^2 + |\overline{H_n R_n}|^2 \,\,\, | – |\overline{C H_n}|^2 \\
|\overline{H_n R_n}|^2 &= |\overline{C R_n}|^2 – |\overline{C H_n}|^2 \\
&= 7,6^2 – ( 6 – x )^2 \\
&= 57,8 – (36 – 12x + x^2) \\
&= 57,8 – 36 + 12x – x^2 \\
&= -x^2 + 12x + 21,8 \,\,\, |\sqrt{}\\
&\Rightarrow |\overline{H_n R_n}| = \sqrt{-x^2 +12x + 21,8} cm \end{align}
4.7 Um zu zeigen, dass es dieses Winkelmaß nicht gibt, bestimmst du den kleinsten Winkel, der auftritt. Dieser entsteht, wenn x = 0 ist und der Punkt H auf A liegt.
\begin{align} cos(\angle R_n C A ) &= \frac{|\overline{AC}|}{|\overline{CR_n}|}\\
&= \frac{6}{7,6} \,\,\, |cos^{-1} \\
&\Rightarrow \angle R_n CA = 37,9° \end{align}
Der kleinste Winkel hat 37,9°, also gibt es keinen mit 15°.
