3.1

3.2 Auf hier steht die Höhe senkrecht,. Im Dreieck AMS ist \( |\overline{AS}| \) die Hypotenuse. Der richtige Ansatz ist inzwischen bestimmt kein Problem mehr.
\begin{align}
|\overline{AS}|^2 &= |\overline{AM}|^2 + |\overline{MS}|^2 \\
&= 9^2 + 5^2 \,\,\, |\sqrt{}\\
&\Rightarrow |\overline{AS}| = 10,3 cm \\
\\
tan(\angle MAS) &= \frac{|\overline{MS}|}{|\overline{AM}|} \\
&= \frac{5}{9} \,\,\, |tan^{-1}\\
&\Rightarrow \angle MAS = 29,1° \end{align}
3.3
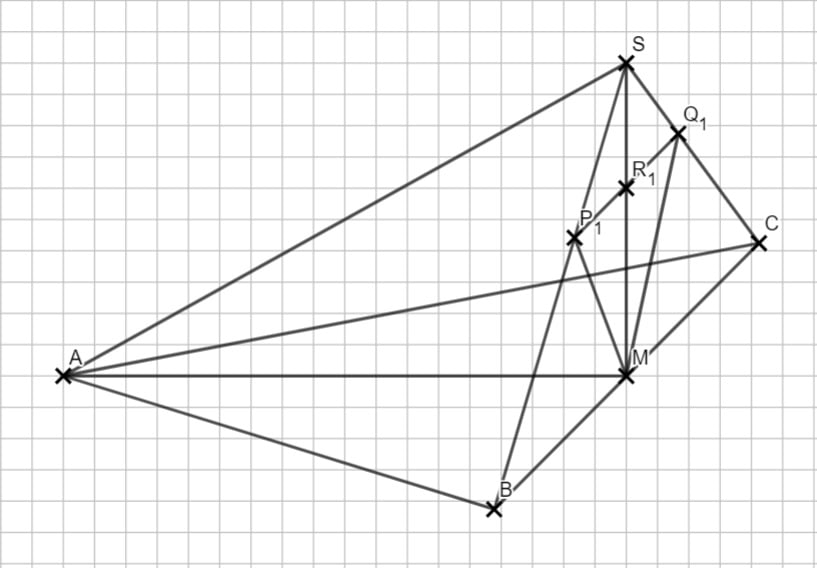
2.4 Wir fangen wieder mit der Flächenformel an: \( A = \frac{1}{2} \cdot g \cdot h \)). Die Höhe des Dreiecks ist die gesamte Höhe der Pyramide minus die Verkürzung, also 2x. Die Grundseite – also die kurze Parallele – musst du mit dem Vierstreckensatz berechnen.
\begin{align}
\frac{|\overline{P_n Q_n}|}{|\overline{BC}|} &= \frac{\overline{S R_n}|}{|\overline{MS}|} \\
\frac{|\overline{P_n Q_n}|} {12} &= \frac{2x}{5} \,\,\, |\cdot 12 \\
|\overline{P_n Q_n}| &= \frac{2x}{5} \cdot 12 \\
&\Rightarrow |\overline{P_n Q_n}| = 4,8x \\
\\
h &= |\overline{MR_n}| = |\overline{MS}| – |\overline{SR_n}| = 5 – 2x \\
\\
A &= \frac{1}{2} \cdot g \cdot h \\
&= \frac{1}{2} \cdot |\overline{P_n Q_n}| \cdot |\overline{M R_n}|\\
&= \frac{1}{2} \cdot (4,8x) \cdot (5-2x) \\
&= 2,4x \cdot (5 -2x) \\
\Rightarrow &A = -12x – 4,8x^2 = (-4,8x^2 – 12x) cm^2 \end{align}
3.5 Taschenrechnereingabe gehört zum Lösungsweg. Inzwischen bestimmt klar!
\begin{align} &\text{Menü} \Rightarrow A \Rightarrow 1 \Rightarrow 2 \Rightarrow -4,8x² + 12x \Rightarrow A_{max} = 7,5 cm^2 \text{ für } x = 1,25 \end{align}
3.6 Achtung, es geht hier nicht um allgemeine Winkel, sondern um den Winkel aus 3.5. Du weißt also, dass es um den Winkel im größten Dreieck geht. Hier ist x = 1,25. Mit diesem Wert von x kannst du die Katheten im Dreieck MRP ausrechen und mit dem Tangens den Winkel bei M berechnen. Jetzt noch mal 2 und du hast es geschafft!
\begin{align} |\overline{MR_0}|&= 5 – 2x = 5 – 2 \cdot 1,25 = 2,5 cm\\
|\overline{P_0 Q_0}| &= 4,8x = 4,8 \cdot 1,25 = 6cm \\
&\Rightarrow |\overline{P_0 R_0}| = 3 cm \\
\\
tan(\angle R_0 M P_0) &= \frac{|\overline{P_0 R_0}|}{|\overline{MR_0}|} \\
&= \frac{3}{2,5} \,\,\, |tan^{-1} \\
\angle R_0 M P_0 &= 50,2° \\
\Rightarrow &\angle Q_0 M P_0 = 100,4° \end{align}
