2.1
2.2 Die Höhe steht immer senkrecht, also entstehen rechtwinklige Dreiecke. Im Dreieck CMS ist \( |\overline{CS}| \) die Hypotenuse. Jetzt musst du nur den richtigen Ansatz finden.
\begin{align}
|\overline{CS}|^2 &= |\overline{CM}|^2 + |\overline{MS}|^2 \\
&= 5^2 + 5^2 \,\,\, |\sqrt{}\\
&\Rightarrow |\overline{CS}| = 7,1 cm \\
\\
tan(\angle SCA) &= \frac{|\overline{MS}|}{|\overline{CM}|} \\
&= \frac{5}{5} \,\,\, |tan^{-1}\\
&\Rightarrow \angle CAS = 45,0° \end{align}
2.3
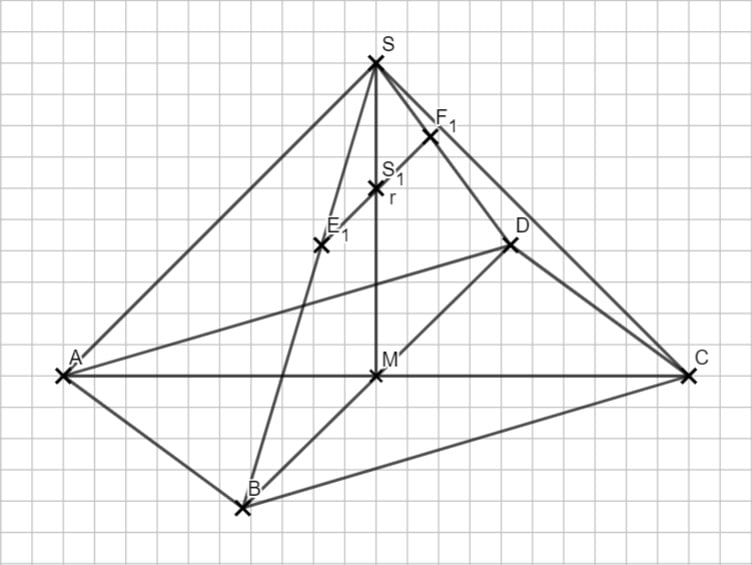
2.4 Diese Aufgaben sind immer schwierig. Deshalb langsam, aber sicher! Zuerst die Flächenformel des Trapezes (\( A = \frac{a+c}{2} \cdot h \)). Die Höhe des Trapezes ist also x. Die kurze Parallele musst du mit dem Vierstreckensatz berechnen.
\begin{align} \frac{|\overline{E_n F_n}|}{|\overline{BD}|} &= \frac{\overline{S S_n}|}{|\overline{MS}|} \\
\frac{|\overline{E_n F_n}|} {12} &= \frac{5 – x}{5} \,\,\, |\cdot 12 \\
|\overline{E_n F_n}| &=\frac{5 – x}{5} \cdot 12 \\
|\overline{E_n F_n}| &=(1 – \frac{x}{5}) \cdot 12 \\
|\overline{E_n F_n}| &=12 – 2,4x \\
&\Rightarrow |\overline{E_n F_n}| = -2,4x + 12 \\
\\
A &= \frac{a + c}{2} \cdot h \\
&= \frac{|\overline{E_n F_n}| + |\overline{BD}|}{2} \cdot |\overline{M S_n}| \\
&= \frac{-2,4x + 12 + 12}{2} \cdot x\\
&=\frac{-2,4x + 24}{2} \cdot x \\
&(-1,2x + 12) \dot x \\
&\Rightarrow A = (-1,2x^2 + 12x) cm^2 \end{align}
2.5 Nicht vergessen aufzuschreiben, was du in den Taschenrechner eingibst. Das gehört mit zum Lösungsweg!
\begin{align} &\text{Menü} \Rightarrow A \Rightarrow 1 \Rightarrow 2 \Rightarrow -1,2x² + 12x \Rightarrow A_{max} = 30 cm^2 \text{ für } x = 5 \end{align}
Dieser Wert ist nicht erlaubt, da er nicht im Intervall von Aufgabe 2.3 steht. Je näher der Wert an 5 heran kommt, desto größer wird der Flächeninhalt. Der größte Wert wird aber nie erreicht.
2.6 Auch hier spielen wieder besondere Winkel eine Rolle. Erinnerst du dich noch an den Ergänzungswinkel? Die nebeneinanderliegenden Winkel in einem Trapez ergeben zusammen 180°. Hier ist das auch so, auch wenn man es im Schrägbild nur schwer erkennt.
\begin{align} \angle MBS \text{ und } \angle BE_n F_n &\text{ sind Ergänzugswinkel, also gilt:}\\
\angle MBS + \angle BE_n F_n &= 180° \\
\\
\text{ Jetzt berechnest du den Winkel MBS im Dreieck BMS}\\
tan(\angle MBS) &= \frac{|\overline{MS}|}{|\overline{BM}|}\\
&= \frac{5}{6} \,\,\, |tan^{-1}\\
&\Rightarrow \angle MBS = 39,8°\\
\\
39,8° + \angle BE_n F_n &= 180° \,\,\, |-39,8° \\
\angle BE_n F_n &= 140,2° \end{align}
Der Winkel ist immer 140,2°, egal wo En ist.
