1.1
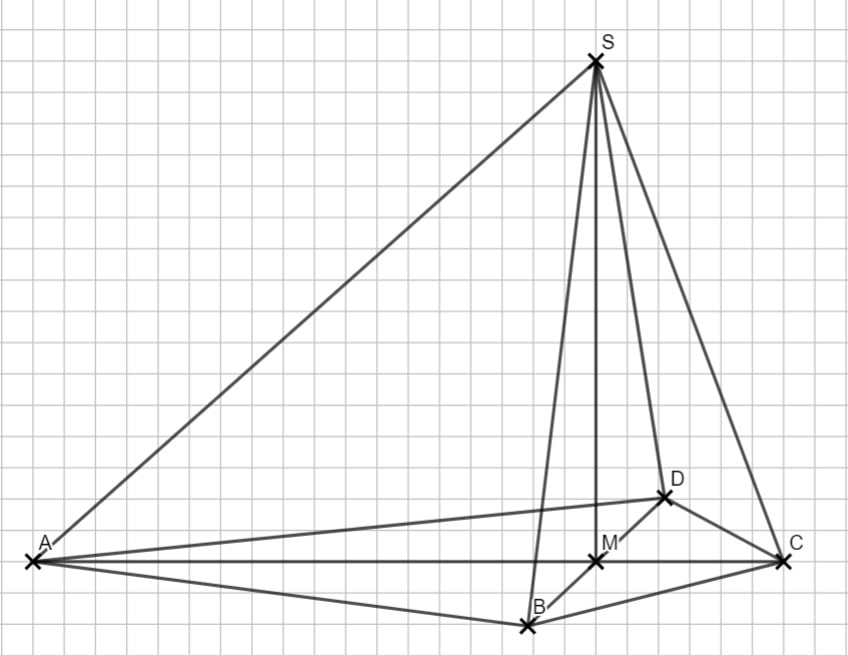
1.2 Die Höhe steht immer senkrecht, also entstehen rechtwinklige Dreiecke. Im Dreieck AMS ist \( |\overline{AS}| \) die Hypotenuse. Jetzt musst du nur den richtigen Ansatz finden.
\begin{align}
|\overline{AS}|^2 &= |\overline{AM}|^2 + |\overline{MS}|^2 \\
&= 9^2 + 8^2 \,\,\, |\sqrt{}\\
&\Rightarrow |\overline{AS}| = 12,0 cm \\
\\
tan(\angle CAS) &= \frac{|\overline{MS}|}{|\overline{AM}|} \\
&= \frac{8}{9} \,\,\, |tan^{-1}\\
&\Rightarrow \angle CAS = 41,6° \end{align}
1.3 Gehe von der Spitze S drei Zentimeter auf der Kante AS entlang. Ergänze dann mit passenden Punkten zum Rechteck. Denke daran, deine Punkte zu beschriften!
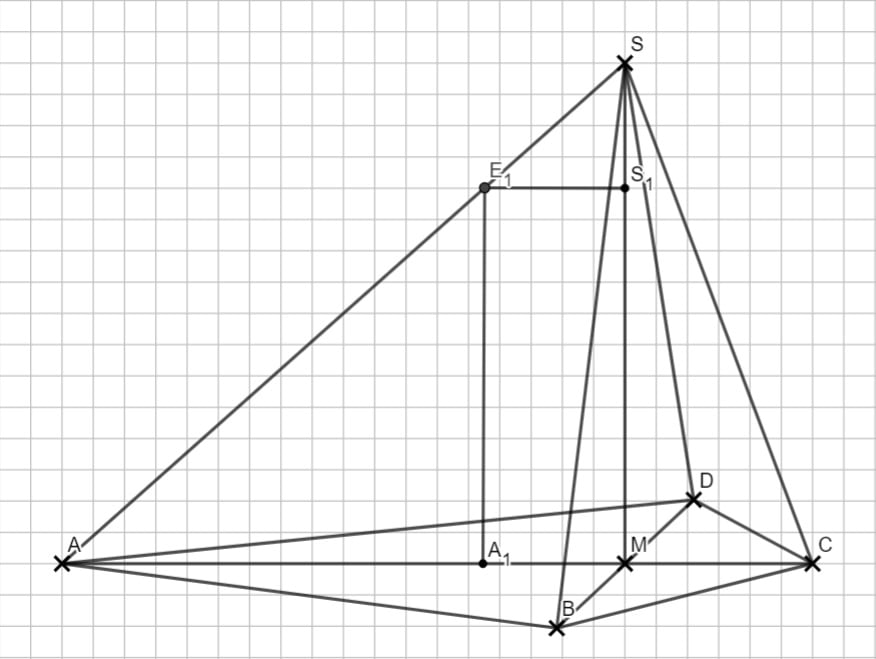
1.4 Jetzt wird es kompliziert. Die Flächenformel für das Rechteck ist A = l*b. Die Länge und die Breite kannst du jeweils mit dem Vierstreckensatz innerhalb des Dreiecks AMS ausrechnen. Genau hinschauen, ist nicht einfach! Immer Parallele/Parallele = Seite/Seite
\begin{align} \frac{|\overline{AE_n}|}{|\overline{AS}|} &= \frac{\overline{A_n E_n}|}{|\overline{MS}|} \\
\frac{12- x } {12} &= \frac{|\overline{A_n E_n}|}{8} \,\,\, |\cdot 8 \\
\frac{12-x}{12} \cdot 8 &= |\overline{A_n E_n}| \\
&\Rightarrow |\overline{A_n E_n}| = 8 – \frac{2}{3}x = -\frac{2}{3}x + 8 \\
\\
\frac{|\overline{SE_n}|}{|\overline{AS}|} &= \frac{\overline{S_n E_n}|}{|\overline{AM}|} \\
\frac{x} {12} &= \frac{|\overline{S_n E_n}|}{9} \,\,\, |\cdot 9 \\
&\Rightarrow |\overline{S_n E_n}| = 0,75x\\
\\
A &= l \cdot b \\
&= (-\frac{2}{3}x + 8) \cdot 0,75x \\
&= -0,5x^2 + 6x \end{align}
1.5 Nicht vergessen aufzuschreiben, was du in den Taschenrechner eingibst. Das gehört mit zum Lösungsweg!
\begin{align} &\text{Menü} \Rightarrow A \Rightarrow 1 \Rightarrow 2 \Rightarrow -0,5x² +6x \Rightarrow A_{max} = 18 cm^2 \text{ für } x = 6 \end{align}
1.6 Ein Rechteck wird zum Quadrat, wenn Länge und Breite gleich sind. Setzte die Terme gleich und löse die Gleichung.
\begin{align} \text{Länge} &= \text{Breite} \\
0,75 x &= – \frac{2}{3}x + 8 \,\,\, + \frac{2}{3} x \\
1,4x &= 8 \,\,\, |:1,4\\
x &= 5,7\\
\\
\text{Einsetzen in die Formel aus 1.4}\\
A(5,7) &= -0,5 \cdot (5,7)^2 + 6 \cdot 5,7 = 18,0 cm^2 \end{align}