Übung 1: Kreatives Fahrrad
Die Reifen des Fahrrads bestehen in der Mitte aus gleichseitigen Dreiecken, über dessen Seiten Kreisbögen gezogen wurden. Der Mittelpunkt dieser Kreisbögen ist die gegenüberliegende Ecke des Dreiecks. Bei einer Umdrehung wird also 3 mal der Kreisbogen gefahren. Am Schienbein kannst du abschätzen, dass die Seite des Dreiecks ~0,5m sind. Die Winkel sind im gleichseitigen Dreieck alle 60°.

\begin{align} \text{Ein Bogen} b &= \frac{60°}{360°} \cdot 0,5 \cdot 2 \cdot \pi = 0,52 \\
\text{Eine Radumdrehung} U & 3 \cdot 0,52 = 1,56\\
\text{10 Umdrehungen} U_{ges} &= 10 \cdot 1,56 = 15,6 m \end{align}
Das Fahrrad bewegt sich dann ~16m.
Übung 2: Künstlerische Fallrohre
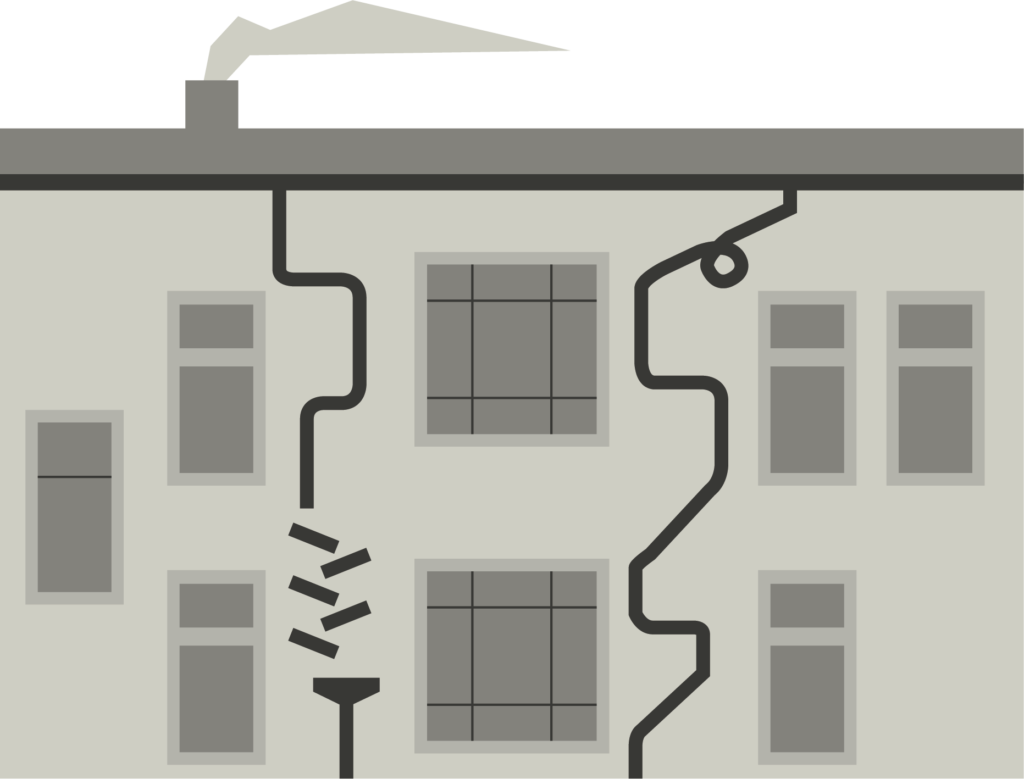
Ein Stockwerk kann als 3 Meter abgeschätzt werden. Damit bekommst du einen Maßstab für die Zeichnung. Das Haus hat 2 Stockwerke und ist 4 cm hoch. 6m entsprechen 4 cm, also ist 1 cm 1,5m. Das „normale“ Fallrohr wäre 6 Meter lang. Jetzt muss du alle Längen im Kunstfallrohr messen und addieren.
Das Fallrohr auf der linken Seite sind ~ 6cm. In Wirklichkeit sind es also 9m.
Auf der rechten Seite sind es ebenfalls ~6 cm, also auch 9m.
Insgesamt sind es 18m Material gegenüber 12m. Das sind 6 Meter mehr Material. 6 von 12 entspricht 50%. Es sind also 50% mehr Material.
Übung 3: Werbeversprechen
Im Bild können wir nichts abschätzen, da bleibt uns nur das Internet. Eine normale Rolle hat einen Durchmesser von 10 – 12 cm, ein Blatt hat eine Breite von 10 cm.
Damit haben wir Zahlen für kleine und große Rollen und machen uns an die Verpackung. Es ist die Oberfläche eines Quaders. Ja, in Wirklichkeit sind die Ecken abgerundet, aber wir sollen hier ja nur schätzen. Du musst jetzt also für beide Quader
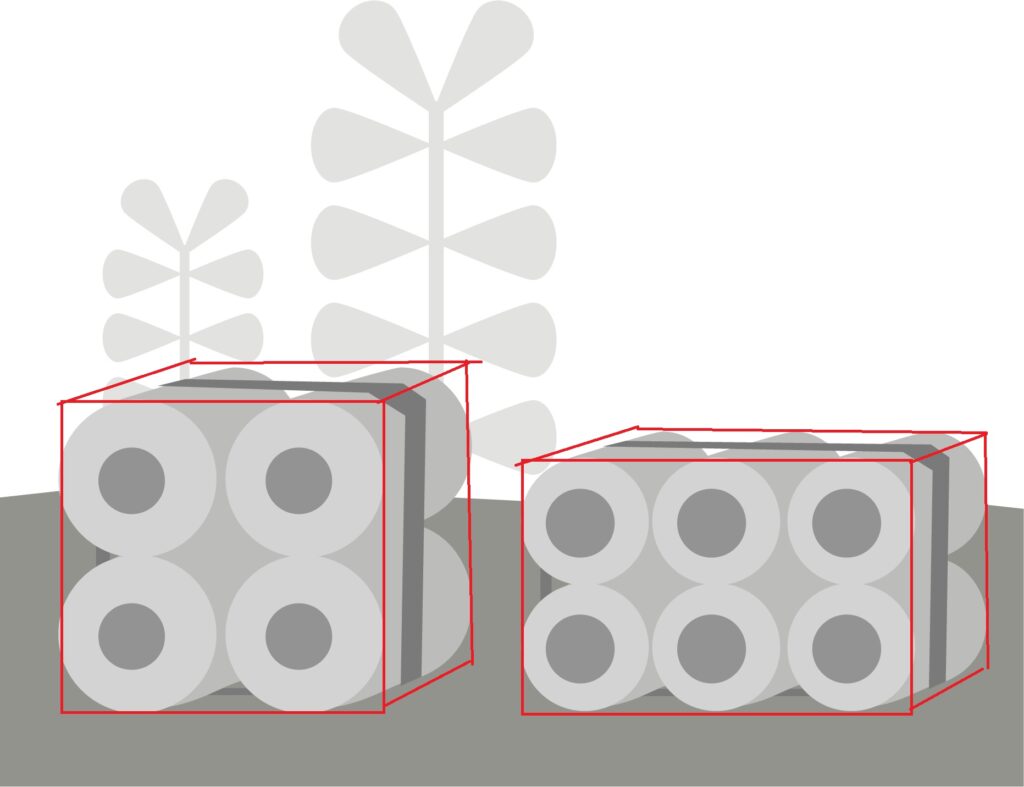
Links d = 12cm, rechts d = 10 cm. Beide haben eine Breite von 10 cm.
\begin{align} \text{Maße links}: l &= 24 cm; b = 10 cm ; h = 24 cm \\
A_{vorne} &= l \cdot h = 24 \cdot 24 = 578 cm^2 \\
A_{unten} &= l \cdot b = 24 \cdot 10 = 240 cm^2 \\
A_{rechts} &= b \cdot h = 10 \cdot 24 = 240 cm^2 \\
A_{ges} &= 1056 cm^2 \\
\\
\text{Maße rechts}: l &= 30 cm ; b = 10 cm ; h = 20cm \\
A_{vorne} &= l \cdot h = 30 \cdot 20 = 600 cm^2 \\
A_{unten} &= l \cdot b = 30 \cdot 10 = 300 cm^2 \\
A_{rechts} &= b \cdot h = 10 \cdot 20 = 200 cm^2 \\
A_{ges} &= 1100 cm^2 \\
\end{align}
Die Ergebnisse sind fast identisch. Das Werbeversprechen lässt sich nicht durch die Pastikverpackung begründen.
Übung 4: Ei am Strand
Iim Bild kannst du den Mensch als 1,8m abschätzen. Dieser passt zweimal in den Durchmesser eines Eis. Das Ei ist also in Wirklichkeit 2,6m breit. Ein Spiegelei schätze ich als Durchmesser 13 cm. Ein Huhn schätze ich auf 40 cm.
Damit ist ein Huhn ungefähr 3 Mal so groß wie das Spielei breit. Aus den 2,6m Kunstspiegelei wird ein dreimal so großes Kunsthuhn:
Das Huhn hätte eine Größe von ungefähr 7,8 Metern.
Übung 5: Gigantische Gabel
Im Bild ist ein Rucksack an dem du die Größe der Gabel abschätzen kannst. Mein Rucksack hat eine Höhe von 60 cm. In die Gabel passt der Rucksack ungefähr 3,5 mal rein. Die Gabel hat also eine Größe von 210 cm.
Eine echte Gabel schätze ich auf 20 cm, die Körpergröße eines Menschen auf 180cm. Ein Mensch ist also 9 mal größer als eine Gabel.
Der Mensch, der die 210 cm Gabel verwendet, ist 210*9cm = 1890 cm also ungefähr 19m groß.
Übung 6: Fußballschuhe
Inzwischen ist der erste Schritt bestimmt klar: Der Mensch ist 1 cm und wir schätzen ihn als 180cm. Die Schuhe sind 5,5 cm breit, also 990cm in Wirklichkeit. Bei den Schuhgrößen kommt das Internet ins Spiel: Der Abstand zwischen zwei Schuhgrößen beträgt 0,66 cm. Eine Größe 40 hat eine Länge von 25,3 cm. Von den 990cm bleiben 965,7 cm. Diese Teilen wir durch die 0,66, um die Anzahl der Vergrößerungen auszurechnen.
\(\) 965,7/0,66 = 1461,6… \(\)
Die Schuhe sind 1464,5 Größen größer als 40. Die Schuhe haben also die Größe 1504,5.
