4.1 Berechne zuerst die Steigung mit der Formel aus der Formelsammlung. Setze dann m und die Koordinaten eines gegebenen Punkes in die Funktionsgleichung ein.
\begin{align} m &= \frac{y_{P_2} – y_{P_1}}{x_{P_2} – x_{P_1}} = \frac{1 – 1,5} {-4 – (-6)} = \frac{-0,5}{2} = -0,25 \\
\\
y &= m \cdot x + t \,\,\, \,\,\, \,\,\, \text{ Setze m = -0,25 ein} \\
y &= -0,25 \cdot x + t \,\,\, \,\,\, \,\,\, \text{ Die Koordinaten eines gegebenen Punktes einsetzen} \\
1 &= -0,25 \cdot (-4) + t \,\,\, \\
1 &= 1 + t \,\,\, | -1 \\
0 &= t \\
&\Rightarrow y = -0,25x \end{align}
4.1 + 4.2
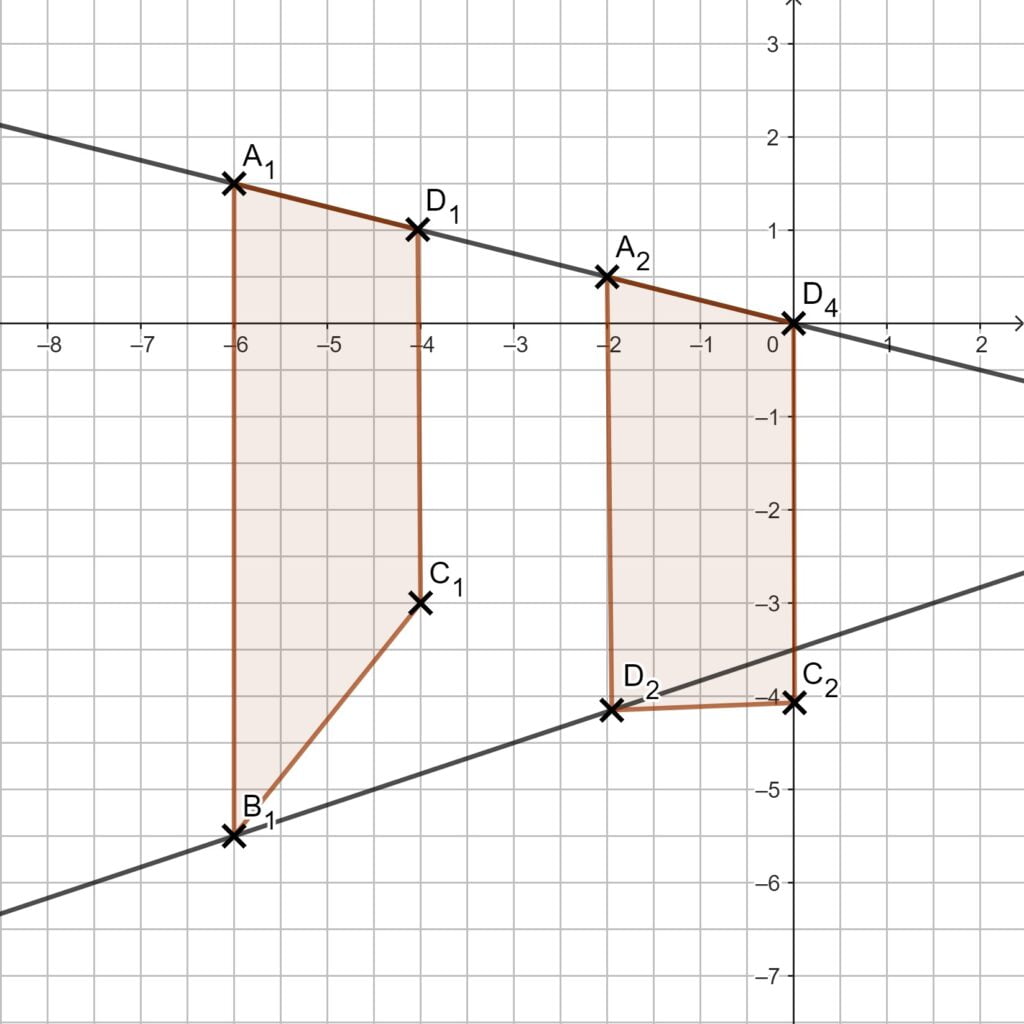
4.3 Setze die beiden Funktionsterme gleich und löse anschließend die Gleichung. Achtung, welche Werte sind hier erlaubt?
\begin{align} y_g &= y_q \\
-0,25x &= \frac{1}{3} x – 3,5 \,\,\ |-\frac{1}{3} x\\
-0,58x &= – 3,5 \,\,\, |:(-0,58)\\
x &= 6,03 \\
x \in \text{]} – \infty ; 6,03 \text{[} \end{align}
Achtung! Hier sind die Punkte links vom Schnittpunkt erlaubt – schaue einfach mal in die Zeichnung.
4.4 Schreibe die Flächenformel einmal allgemein auf und bestimme die Längen anschließend. Längen „mit gleicher Abszisse“ berechnest du durch „Oben – unten“. Anschließend in die Flächenformel einsetzen und vereinfachen.
\begin{align} A &= 0,5 \cdot (a + c) \cdot h = 0,5 \cdot ( |\overline{A_n B_n}| + |\overline{C_n D_n}|) \cdot h \\
\\
h &= 2 LE \,\,\, \,\,\, \,\,\, \,\,\, \text{Aus Aufgabe 4.2: Die Abszisse von D ist immer um 2 größer} \\
|\overline{C_n D_n}| &= 4 LE \,\,\, \,\,\, \,\,\, \,\,\, \text{Aus Aufgabe 4.2} \\
|\overline{A_n B_n} & = „oben \, – \, unten“ \\
&= -0,25x – (\frac{1}{3}x – 3,5) \\
&= –0,25x – \frac{1}{3}x + 3,5 \\
&\Rightarrow |\overline{A_n C_n}| = -0,58x + 3,5 \\
\\
A &= = 0,5 \cdot ( |\overline{A_n B_n}| + |\overline{C_n D_n}|) \cdot h \\
& = 0,5 \cdot (-0,58x + 3,5 + 4) \cdot 2 \\
&= 0,5 \cdot (-0,58x + 7,5) \cdot 2 \\
&\Rightarrow A = (-0,58x + 7,5) FE \end{align}
4.5 Setze die Flächenformel aus 4.4 mit dem vorgebenen Wert gleich und löse die Gleichung. Überprüfe, ob der Wert im erlaubten Intervall aus 3.3 liegt.
\begin{align} -0,58x + 7,5 &= 40 \,\,\, |-7,5 \\
-0,58x &= 32,5 \,\,\, |:(-0,58) \\
x &= -56,03 \\
\text{Der Wert ist erlaubt, denn } -56,03 &< 6,03 \end{align}
4.6 In diesem Fall entsteht ein Parallelgramm, wenn \( |\overline{A_n B_n}| = |\overline{C_n D_n}|\) gilt. Löse diese Gleichung und prüfe, ob der Wert im erlaubten Intervall aus 4.3 liegt.
\begin{align} |\overline{A_n B_n}| &= |\overline{C_n D_n}| \\
-0,58x + 3,5 &= 4 \,\,\, |-3,5 \\
-0,58x &= 0,5 \,\,\, |:(-0,58) \\
x &= -0,86 \end{align}
Für x = -0,86 entsteht ein Parallelogramm
3.7 Überlege dir, wie du den Punkt C eingezeichnet hast! Von A aus geht man 2 LE auf der Gerade entlang. Dann 4 LE nach unten. Wir starten auf der x-Achse.
\begin{align} A(x | -0,25x) &\Rightarrow A_3 (0| 0) \\
\text{2 auf der Gerade entlang:} &\Rightarrow D_3(2|-0,25 \cdot 2) \Rightarrow D_3(2|-0,5) \\
\text{Um 4 LE nach unten:} &\Rightarrow C_3(2|-4,5) \end{align}
