3.1 Berechne zuerst die Steigung mit der Formel aus der Formelsammlung. Setze dann m und die Koordinaten eines gegebenen Punkes in die Funktionsgleichung ein.
\begin{align} m &= \frac{y_{P_2} – y_{P_1}}{x_{P_2} – x_{P_1}} = \frac{9 – 7} {4,5 – 1,5} = \frac{2}{3} \\
\\
y &= m \cdot x + t \,\,\, \,\,\, \,\,\, Setze \, m = \frac{2}{3} \, ein \\
y &= \frac{2}{3} \cdot x + t \,\,\, \,\,\, \,\,\, \text{ Die Koordinaten eines gegebenen Punktes einsetzen} \\
7 &= \frac{2}{3} \cdot 1,5 + t \,\,\, \\
7 &= 1 + t \,\,\, |-1 \\
6 &= t \\
&\Rightarrow y = \frac{2}{3}x + 6 \end{align}
3.1 + 3.2
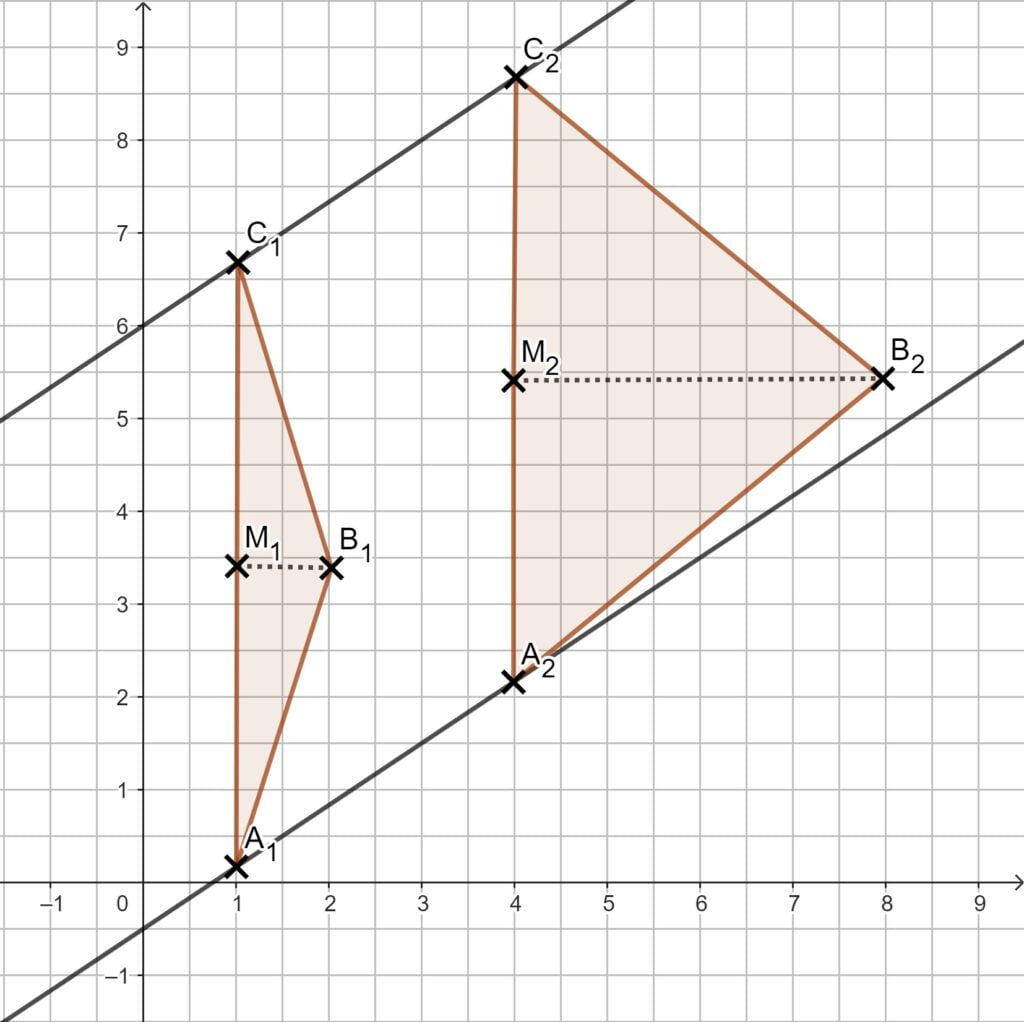
3.3 Setze die beiden Funktionsterme gleich und löse anschließend die Gleichung. Es tritt ein Sonderfall auf!
\begin{align} y_g &= y_q \\
\frac{2}{3}x + 6 &= \frac{2}{3}x – 0,5 \,\,\, | – \frac{2}{3}x \\
6 & = -0,5 \end{align}
Es entsteht eine falsche Aussage. Es gibt also keinen Schnittpunkt. Damit finden wir hier keinen problematischen Bereich. Weil aber die Höhe des Dreieck x cm ist und nicht 0 oder negativ werden darf, gilt: \( x \in \text{]} 0 ; \infty \text{[} \) .
3.4 Schreibe die Flächenformel einmal allgemein auf und bestimme die Längen anschließend. Längen „mit gleicher Abszisse“ berechnest du durch „Oben – unten“. Anschließend in die Flächenformel einsetzen und vereinfachen.
\begin{align} A &= 0,5 \cdot g \cdot h = 0,5 \cdot |\overline{A_n C_n}| \cdot |\overline{M_n B_n}| \\
\\
|\overline{M_n B_n}| &= x LE \,\,\, \,\,\, \,\,\, \,\,\, \text{Aus Aufgabe 3.2} \\
|\overline{A_n C_n} & = „oben \, – \, unten“ \\
&= \frac{2}{3}x + 6 – (\frac{2}{3}x -0,5) \\
&= \frac{2}{3}x + 6 – \frac{2}{3}x +0,5) \\
&\Rightarrow |\overline{A_n C_n}| = 6,5 \\
\\
A &= 0,5 |\overline{A_n C_n}| \cdot |\overline{M_n B_n}| \\
& = 0,5 \cdot 6,5 \cdot x \\
&\Rightarrow A = 3,25x FE \end{align}
3.5 Setze die Flächenformel aus 3.4 mit dem vorgebenen Wert gleich und löse die Gleichung. Überprüfe, ob der Wert im erlaubten Intervall aus 3.3 liegt.
\begin{align} 3,25x &= 7,5 \,\,\, |:3,25 \\
x &= 2 \\
\text{Der Wert ist erlaubt, denn } 2 &> 0 \end{align}
3.6 Achtung Sonderfall! Hier ist nicht der gesuchte Wert als Zahl gegeben, sondern als Eigenschaft. Wenn das Dreieck gleichseitig ist, dann gilt auch die Formel des gleichseitigen Dreieck. Schaue dazu in die Formelsammlung! Weil gilt: \( |\overline{A_n C_n}| = 6,5 cm\) und zwar immer, muss das die Seitenlänge sein, für die das gleichseitige Dreieck entsteht. Berechne für 6,5 den Flächeninhalt mit der Formel aus der Formelsammlung und setze mit der Formel aus 3.4 gleich. Löse dann die Gleichung und prüfe, ob der Wert im erlaubten Intervall aus 3.3 liegt.
\begin{align} A &= \frac{\sqrt{3}}{4} \cdot a^2 = \frac{\sqrt{3}}{4} \cdot 6,5^2 = 18,29 cm^2 \\
\\
A(x) &= A \\
3,25x &= 28,17 \,\,\, |:3,25 \\
x &= 5,63 \end{align}
Für x = 5,63 entsteht ein gleichseitiges Dreieck.
3.7 Überlege dir, wie du den Punkt B eingezeichnet hast! Auf halber Höhe zwischen A und C und dann x nach rechts. Genau diesen Weg musst du rechnen. Du kannst die Formel für den Mittelpunkt verwenden oder von A 3,25 auf die y-Koordinate addieren, denn das ist die halbe Streckenlänge.
\begin{align} A(x | \frac{2}{3} x – 0,5) &\Rightarrow A_3 (5,63| \frac{2}{3} \cdot 5,63 – 0,5) \Rightarrow A_3 (5,63|3,25) \\
\text{Um 3,25 nach oben} &\Rightarrow M_3(5,63|6,5) \\
\text{Um x =5,63 nach rechts} &\Rightarrow B_3(11,26|6,5) \end{align}
