2.1 Berechne zuerst die Steigung mit der Formel aus der Formelsammlung. Setze dann m und die Koordinaten eines gegebenen Punkes in die Funktionsgleichung ein.
\begin{align} m &= \frac{y_{P_2} – y_{P_1}}{x_{P_2} – x_{P_1}} = \frac{-4 – 0} {2 -(-2)} = \frac{-4}{4} = – 1 \\
\\
y &= m \cdot x + t \,\,\, \,\,\, \,\,\, \text{ Setze m = -1 ein} \\
y &= -1 \cdot x + t \,\,\, \,\,\, \,\,\, \text{ Die Koordinaten eines gegebenen Punktes einsetzen} \\
0 &= -1 \cdot (-2) + t \,\,\, \\
0 &= 2 + t \,\,\,\,\,\, |-2 \\
– 2 &= t \\
&\Rightarrow y = -x -2 \end{align}
2.1 + 2.2
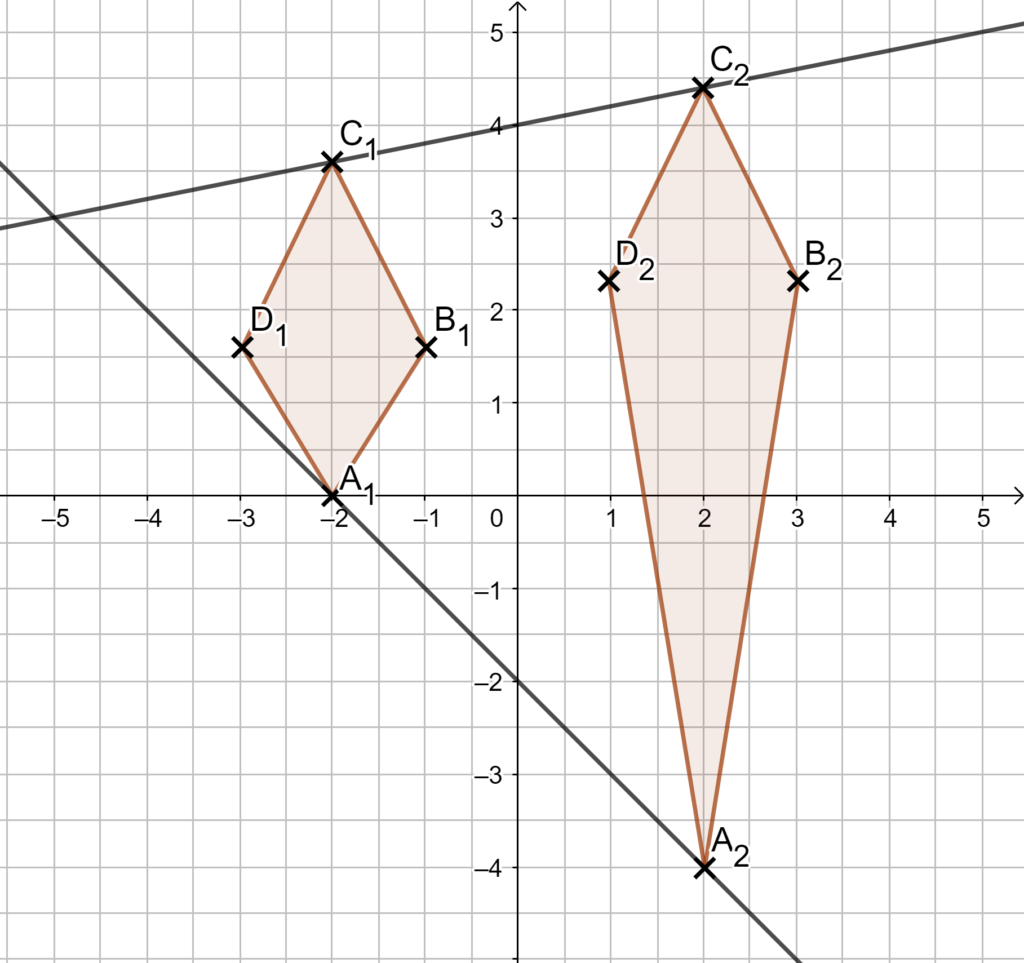
2.3 Setze die beiden Funktionsterme gleich und löse anschließend die Gleichung. Überlege dir, ob die erlaubten Werte links oder rechts vom Schnittpunkt liegen.
\begin{align} y_g &= y_q \\
-x – 2 &= 0,2x + 4 \,\,\, |-0,2x \\
-1,2x – 2 &= 4 \,\,\, |+2 \\
-1,2x &= 6 \,\,\, |:(-1,2) \\
x &= -5 \\
&\Rightarrow x \in \text{]} -5 ; \infty \text{[} \end{align}
2.4 Schreibe die Flächenformel einmal allgemein auf und bestimme die Längen anschließend. Längen „mit gleicher Abszisse“ berechnest du durch „Oben – unten“. Anschließend in die Flächenformel einsetzen und vereinfachen.
\begin{align} A &= 0,5 \cdot e \cdot f = 0,5 \cdot |\overline{A_n C_n}| \cdot |\overline{B_n D_n}| \\
\\
|\overline{B_n D_n}| &= 2 LE \,\,\, \,\,\, \,\,\, \,\,\, \text{2 mal die x-Koordinate des Vektors aus Aufgabe 2.2} \\
|\overline{A_n C_n} & = „oben \, – \, unten“ \\
&= 0,2x + 4 – (-x – 2) \\
&= 0,2x +4 +x + 2 \\
&\Rightarrow |\overline{A_n C_n}| = 1,2x + 6 \\
\\
A &= |\overline{A_n B_n}| \cdot |\overline{B_n C_n}| \\
& = 0,5 \cdot (1,2x + 6) \cdot 2 \\
&\Rightarrow A = (1,2x + 6) FE \end{align}
2.5 Setze die Flächenformel aus 2.4 mit dem vorgebenen Wert gleich und löse die Gleichung. Überprüfe, ob der Wert im erlaubten Intervall aus 2.3 liegt.
\begin{align} 1,2x + 6 &= 2 \,\,\, |-6 \\
1,2x &= -4 \,\,\, |:1,2 \\
x &= -3,33 \\
\text{Der Wert ist erlaubt, denn } -3,33 &> -5 \end{align}
2.6 Das Dreieck ABD und CDB haben beide die Grundseite \( \overline{BD} \). Das Dreieck ABD ist also doppelt so groß wie ADB, wenn die Höhe doppelt so groß ist. Aus dem Vektor aus 2.2 weißt du, dass das obere Dreieck die Höhe 2 hat. Die Frage ist also wann die Höhe von ABD 4 LE ist. Das ist der Fall, wenn die gesamte Diagonale \( |\overline{A_n C_n}| = 6 cm\) lang ist. Überprüfe dann, ob der Wert im erlaubten Intervall aus 2.3 liegt.
\begin{align} l &= b \\
|\overline{A_n C_n}| &= 6 \\
1,2x + 6 &= 6 \,\,\, | -6 \\
1,2x &= 0 \,\,\, |:1,2 \\
x &=0 \,\,\, (> -5) \end{align}
Für x = 0 hat das untere Dreieck einen doppelt so großen Flächeninhalt wie das obere.
2.7 Berechne zuerst C1 und überlege dir, wie du den Vektor aus 2.2 verändert musst, um du D zu kommen.
\begin{align} C_n(x|0,2x+4) &\Rightarrow C_1(-2|0,2 \cdot (-2) +4) \Rightarrow C_1(-2|-0,4 +4) \Rightarrow C_1(-2|3,6) \\
&\text{x-Koordinaten -1 und y-Koordinate -2} \\
C_1(-2|3,6) &\Rightarrow D_1(-2 -1| 3,6 -2) \Rightarrow D_1(-3|1,6) \end{align}
