1.1 Berechne zuerst die Steigung mit der Formel aus der Formelsammlung. Setze dann m und die Koordinaten eines gegebenen Punkes in die Funktionsgleichung ein.
\begin{align} m &= \frac{y_{P_2} – y_{P_1}}{x_{P_2} – x_{P_1}} = \frac{1,5 – 2} {3 -1} = \frac{-0,5}{2} = -0,25 \\
\\
y &= m \cdot x + t \,\,\, \,\,\, \,\,\, \text{ Setze m = -0,25 ein} \\
y &= -0,25 \cdot x + t \,\,\, \,\,\, \,\,\, \text{ Die Koordinaten eines gegebenen Punktes einsetzen} \\
2 &= -0,25 \cdot 1 + t \,\,\, \\
2 &= – 0,25 + t \,\,\, |+0,25 \\
2,25 &= t \\
&\Rightarrow y = -0,25x + 2,25 \end{align}
1.1 + 1.2
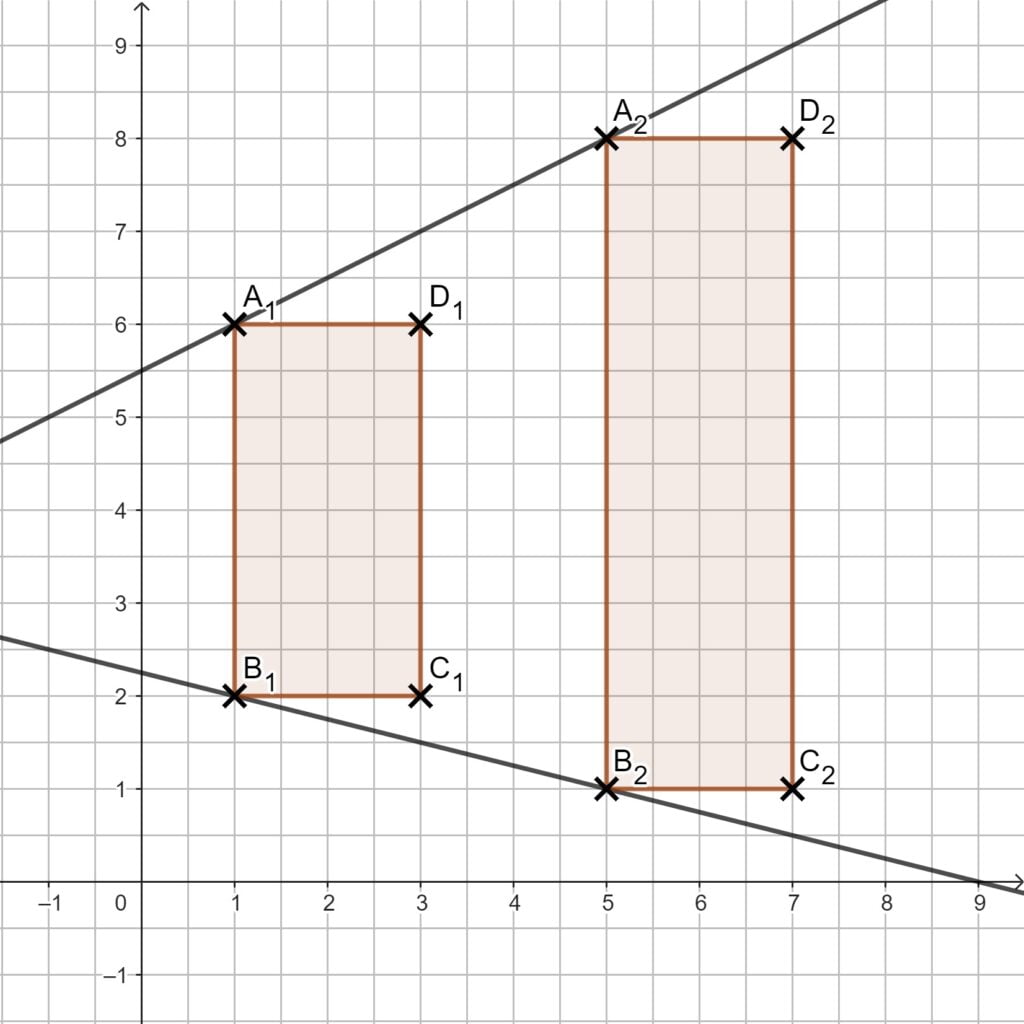
1.3 Setze die beiden Funktionsterme gleich und die löse anschließend die Gleichung. Überlege dir, ob die erlaubten Werte links oder rechts vom Schnittpunkt liegen.
\begin{align} y_g &= y_q \\
-0,25x + 2,25 &= 0,5x + 5,5 \,\,\, |-0,5x \\
-0,75x + 2,25 &= 5,5 \,\,\, |-2,25 \\
-0,75x &= 3,25 \,\,\, |:(-0,75) \\
x &= -4,33 \\
&\Rightarrow x \in \text{]} -4,33 ; \infty \text{[} \end{align}
1.4 Schreibe die Flächenformel einmal allgemein auf und bestimme die Längen anschließend. Längen „mit gleicher Abszisse“ berechnest du durch „Oben – unten“. Anschließend in die Flächenformel einsetzen und vereinfachen.
\begin{align} A &= l \cdot b = |\overline{A_n B_n}| \cdot |\overline{B_n C_n}| \\
\\
|\overline{B_n C_n}| &= 2 LE \,\,\, \text{Aus Aufgabe 1.2} \\
|\overline{A_n B_n} & = „oben \, – \, unten“ \\
&= 0,5x +5,5 – (-0,25x +2,25) \\
&= 0,5x + 5,5 + 0,25x – 2,25 \\
&\Rightarrow |\overline{A_n B_n}| = 0,75x + 3,25 \\
\\
A &= |\overline{A_n B_n}| \cdot |\overline{B_n C_n}| \\
& = (0,75x + 3,25) \cdot 2 \\
&\Rightarrow A = (1,5x + 6,5) FE \end{align}
1.5 Setze die Flächenformel aus 1.4 mit dem vorgebenen Wert gleich und löse die Gleichung .Überprüfe, ob der Wert im erlaubten Intervall aus 1.3 liegt.
\begin{align} 1,5x + 6,5 &= 11 \,\,\, |-6,5 \\
1,5x &= 4,5 \,\,\, |:1,5 \\
x &= 3 \\
\text{Der Wert ist erlaubt, denn } 3 &> -4,33 \end{align}
1.6 Überlege dir, welche Eigenschaft aus einem Rechteckt ein Quadrat macht. Übersetze diese Eigenschaft in eine Gleichung und löse sie. Überprüfe dann, ob der Wert im erlaubten Intervall aus 1.3 liegt.
\begin{align} l &= b \\
|\overline{A_n B_n}| &= |\overline{B_n C_n}| \\
0,75x + 3,25 &= 2 \,\,\, | -3,25 \\
0,75x &= -1,25 \,\,\, |:0,75 \\
x &= – 1,67 \,\,\, (> -4,33) \end{align}
Es gibt ein Qudrat für x = -1,67
1.7Berechne den Punkt A über die Funktionsgleichung und schließe dann durch Verschiebung auf D
\begin{align} A(x|0,5x + 5,5) &\Rightarrow A(-1,67| 0,5 \cdot (-1,67) + 5,5) \, \Rightarrow \, A(-1,67|4,67) \\
A(-1,67|4,67) &\text{ D liegt 2 LE weiter rechts } D(0,33|4,67)\end{align}
