4.1
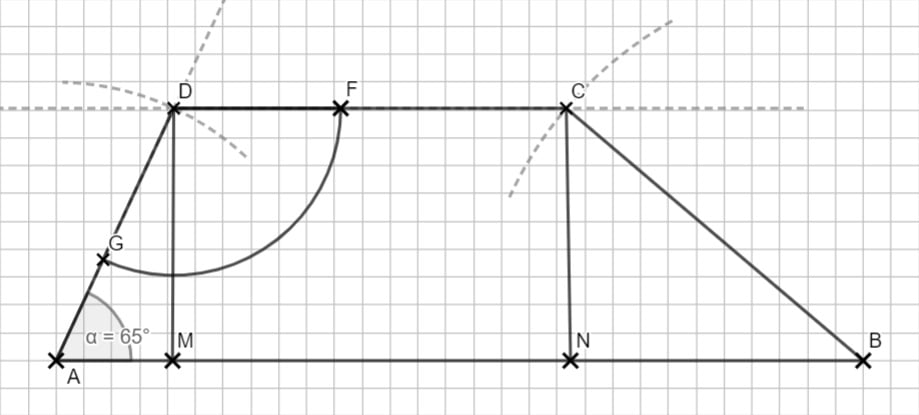
4.2 Die Höhe steht immer senkrecht, also darfst du im Dreieck AED mit Sin/Cos/Tan rechnen.
\begin{align} sin(\angle BAD) &= \frac{h_D}{|\overline{AE}|} \\
sin(65°) &= \frac{h_D}{5} \,\,\, |\cdot 5 \\
&\Rightarrow h_D = 4,5 cm \end{align}
Auf der rechten Seite kannst du die Höhe durch C einzeichnen. Dass du deine Strecken richtig benennen kannst, benenne den Schnittpunkt unten. Ich nenne ihn einfach N.
\begin{align} sin(\angle CBA) &= \frac{h_C}{|\overline{BC}|} \\
sin(\angle CBA) &= \frac{4,5}{7} \,\,\, |sin^{-1} \\
&\Rightarrow \angle CBA = 40,0° \end{align}
4.3 Die gesuche Streckenlänge ist eine der parallelen Seiten im Trapez. Du kannst also die lange Grundseite nehmen und die beiden „Flügelchen“ abziehen. Was übrig bleibt, ist die gesuchte Strecke.
Rechter Flügel:
\begin{align} cos(\angle BAD) &= \frac{|\overline{AE}|}{|\overline{AD}|} \\
cos(65°) &= \frac{|\overline{AE}|}{5} \,\,\, |\cdot 5 \\
&\Rightarrow |\overline{AE}| = 2,1 cm \end{align}
Linker Flügel
\begin{align} tan(\angle CBA) &= \frac{|\overline{h_C}|}{|\overline{BN}|} \\
tan(40°) &= \frac{4,5}{|\overline{BN}|} \,\,\, |\cdot |\overline{BN}| : tan(40°) \\
&\Rightarrow |\overline{BN}| = 5,4 cm \end{align}
Alles – links – rechts
\begin{align}
|\overline{CD}| &= |\overline{AB}| -|\overline{AE}| – |\overline{BN}| \\
&= 14 – 2,1 – 5,4 \\
&\Rightarrow |\overline{CD}| = 6,5 cm \end{align}
4.4 Einfach in die Flächenformel einsetzen. Dafür hast du alle Angaben.
\begin{align} A_{Trapez} &= 0,5 \cdot (|\overline{AB}| + |\overline{CD}| ) \cdot h \\
&= 0,5 \cdot (14 + 6,5) \cdot 4,5 \\
&\Rightarrow A_{Trapez} = 46,1 cm^2 \end{align}
4.5 Hier kommt der Hinweis über der Aufgabe ins Spiel! An zwei parallelen Geraden entstehen Stufen- /Wechsel- und Ergänzungwinkel. Weil ein Trapez zwei parallele Seiten hat, sind innerhalb des Trapezes Ergänzungswinkel. Oder weniger kompliziert: der Winkel bei A und bei D ergeben zusammen 180°. Dasselbe gilt für die Winkel bei B und C. Das muss man jetzt noch sauber aufschreiben.
\begin{align} AB||CD \Rightarrow \angle BAD + \angle ADC &= 180° (\text{Ergänzungswinkel}) \\
65° + \angle ADC &= 180° \,\,\, |-65° \\
\angle ADC &= 115° \end{align}
4.6 \begin{align} A_{Sektor} &= \frac{115°}{360°} \cdot 3^2 \cdot \pi \\
&= 9,0 cm^2 \\
\\
p &= \frac{Anteil}{Ganzes} \cdot 100 \% = \frac{9,0}{46,1} \cdot 100\% = 19,5 \% \end{align}
4.7 Einfach mal probieren die Lösung ohne Text nachzuvollziehen! Wenn das klappt, bist du ready!
\begin{align} |\overline{AN}| &= 2,1 + 6,5 = 8,6 cm \\
\\
tan(\angle ACN) &= \frac{|\overline{AN}|}{|\overline{h_C}|}\\
tan(\angle ACN) & = \frac{8,6}{4,5} \,\,\, |tan^{-1}\\
&\Rightarrow \angle ACN = 62,4° \\
\\
\angle DCA &= 90° – 62,4° = 27,6° \end{align}
