3.1
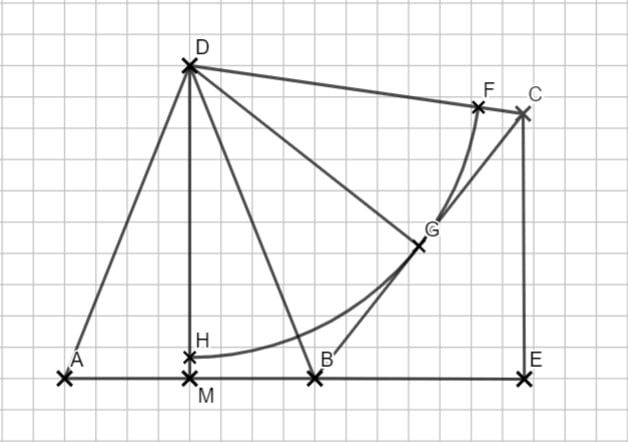
3.2 Die Höhe zerteilt das gleichschenklige Dreieck im rechten Winkel. Bei ist \( \overline{AD}\) die Hypotenuse. Der Rest sollte dann kein Problem mehr sein.
\begin{align} |\overline{AD}| ^2 &= |\overline{AM}|^2 + |\overline{MD}|^2 \\
&= 2^2 + 6^2 \,\,\, |\sqrt{}\\
&\Rightarrow |\overline{AD}| = 6,3 cm \\
\\
tan(\angle BAD) &= \frac{|\overline{MD}|}{|\overline{AM}|}\\
&= \frac{6}{2} \,\,\, |tan^{-1}\\
&\Rightarrow \angle BAD = 71,6° \end{align}
3.3 Gehe wie im Tipp erstmal die Eigenschaften durch, die du kennst. Das Dreieck ABD ist gleichschenklig, also hat es an der Basis gleiche Winkel und die beiden Schenkel ahbe gleiche Länge. Das Dreieck BCD ist gleichseitig, also hat es nur 60° Winkel. Jetzt noch den Winkel EBC berechnen, indem man von 180° die anderen beiden Winkel an der Geraden AE abziehen und fertig! Ja, ist nicht einfach!
\begin{align} |\overline{AD}|&= |\overline{BD}| \text{ (Gleichschenklig)} \\
|\overline{BD}| &= |\overline{BC}| \text{ (Gleichseitig)} \\
&\Rightarrow |\overline{AD}|= |\overline{BC}| = 6,3 cm \\
\\
\angle EBC &= 180° – \angle CBD – \angle DBA \\
&= 180° – 60° – 71,6° \\
&\Rightarrow \angle EBC = 48,4° \\
\\
cos(\angle EBC) &= \frac{|\overline{BE}|}{|\overline{BC}|} \\
cos(48,4°) &= \frac{|\overline{BE}|}{6,3} \,\,\, |cos^{-1} \\
&\Rightarrow |\overline{BE}| = 4,2 cm \end{align}
3.4 Das linke Dreieck ABD kann mit Grundseite und Höhe berechnet werden, für das gleichseitige Dreieck einfach die Formel aus der Formelsammlung verwenden.
\begin{align} A_{ABD} &= 0,5 \cdot 4 \cdot 6 = 12 cm^2 \\
A_{BCD}&= \frac{\sqrt{3} }{4} \cdot 6,3^2 = 17,2 cm^2 \\
A_{ges} &= 12 + 17,2 = 29,2 cm^2 \end{align}
3.5 Auch hier ist wieder geschicktes Arbeiten gefragt! Bei D ist auch im gleichseitigen Dreieck ein 60° Winkel. Dieser wird durch die neue Strecke in 2 30° Winkel geteilt. Du kannst also mit 30° und Sin/Cos/Tan rechnen, weil es einen rechten Winkel gibt.
\begin{align} cos(\angle BDG) &= \frac{|\overline{BG}|}{|\overline{BD}|} \\
cos(30°) &= \frac{|\overline{BG}|}{6,3} \,\,\, |\cdot 6,3 \\
&\Rightarrow |\overline{BG}| = 5,5 cm \end{align}
3.6 Um den Mittelpunktswinkel zu bestimmen, addierst du die 60° des gleichseitigen Dreiecks mit dem halben Winkel an der spitze des gleichschenkligen Dreiecks. Diesen halben Winkel kannst du durch die Innenwinkelsumme bestimmen.
\begin{align} \angle MDB &= 180° – 90° – 71,6° = 18,4° \\
\angle MDF &= 60° + 18,4° \\
\\
A_{Sektor}&= \frac{78,4°}{360°} \cdot 5,5^2 \cdot \pi = 20,7 cm^2 \\
\\
p &= \frac{Anteil}{Ganzes} = \frac{20,7}{29,3} \cdot 100 \% = 70,6 \% \end{align}
3.7 Dass es ein Drachenviereck ist, muss es zwei Paare gleichlanger, nebeneinanderliegender Seiten geben. Oder anders gesagt:
\begin{align} |\overline{BD}| &= |\overline{DC}| \text{ und }|\overline{BE}| = |\overline{EC}| \end{align} muss gelten.
Die erste Gleichung gilt aufgrund der Gleichseitigkeit des Dreiecks. Die Streckenlänge \( |\overline{EB}| = 4,2 cm \) kennen wir schon. Wenn du also noch \( |\overline{EC}| \) berechnest, weißt du bescheid, ob beide Streckenlängen gleich sind.
\begin{align} sin(48,4°) &= \frac{|\overline{EC}|}{6,3} \,\,\, |\cdot 6,3 \\
&\Rightarrow |\overline{EC}| = 4,7 cm \end{align}
Die Strecken sind unterschiedlich lang, also ist es kein Drachenviereck.
