2.1 + Kreisbögen. Achte beim Einzeichnen auf den Umlaufsinn.
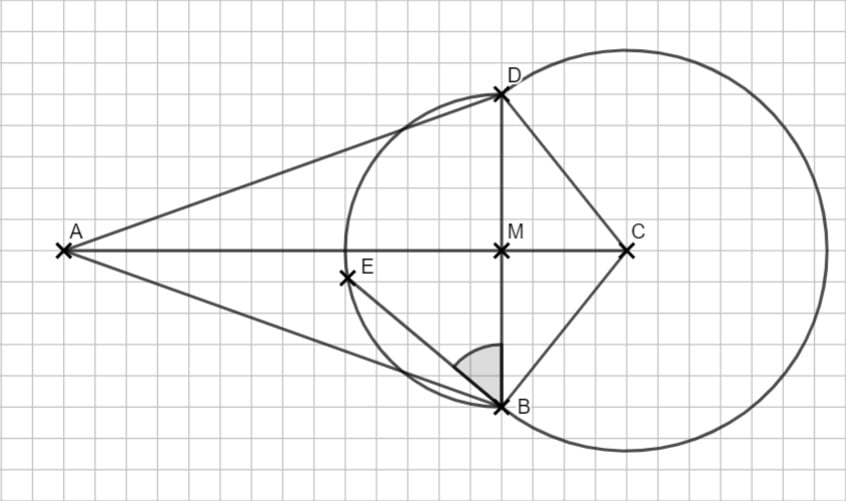
2.2 Die Seiten des Drachenvierecks sind die Hypotenusen der Dreiecke, die mit den Diagonalen entstehen. Du verwendest also zweimal den Satz des Pythagoras und addierst dann.
\begin{align} |\overline{AD}|^2 &= |\overline{AM}|^2 + |\overline{MD}|^2 \\
|\overline{AD}|^2 &= 7^2 + 2,5^2 \,\,\, |\sqrt{}\\
&\Rightarrow |\overline{AD}| = 7,4 cm \\
\\
|\overline{CD}|^2 &= |\overline{MC}|^2 + |\overline{MD}|^2 \\
|\overline{CD}|^2 &= 2^2 + 2,5^2 \,\,\, |\sqrt{}\\
&\Rightarrow |\overline{CD}| = 3,2 cm \\
\\
&\Rightarrow U = 2 \cdot 7,4 + 2 \cdot 3,2 = 21,2 cm
\end{align}
2.3 Der Winkel ADC setzt sich aus den Winkel ADM und MDC zusammen. Für den ersten Teil berechnet man die Winkel und addiert sie.
\begin{align} tan(\angle ADM) &= \frac{|\overline{AM}|}{|\overline{DM}|} \\
&= \frac{7}{2,5} \,\,\, |tan^{-1}\\
&\Rightarrow \angle ADM = 70,3° \\
\\
tan(\angle MDC) &= \frac{|\overline{MC}|}{|\overline{DM}|} \\
&= \frac{2}{2,5} \,\,\, |tan^{-1}\\
&\Rightarrow \angle MDC = 38,7° \\
\\
&\Rightarrow \angle ADC = 70,3° + 38,7° = 109,0° \end{align}
Für den zweiten Teil der Aufgabe brauchst du die Innenwinkelsumme im Viereck. Diese ist ingesamt 360°. Der Winkel ABC ist aufgrund der Symmetrie genauso groß wie ADC. Der Rest ist nicht mehr schwer.
\begin{align} 360° &= \angle CBA + \angle DCB + \angle ADC + \angle BAD \\
360° &= 109,0° + \angle DCB + 109,0° + \angle BAD \,\,\, |-109,0° – 109,0° \\
142,0° &= \angle DCB + \angle BAD \end{align}
2.4 Achtung, in der Mathematik liest man gegen den Uhrzeigersinn. Der Kreis liegt also außerhalb des Drachenvierecks! Ein voller Kreis sind 360° und der Winkel BCD liegt auch außerhalb. Er ist also 360° minus der Winkel bei C im Drachenviereck. Hier steht in sehr kompliziert: Der Winkel innen bei C ist 102,6°. Die Hälfte des gesamten Winkels kannst du mit dem Tangens bestimmen, da bei M ein rechter Winkel ist.
\begin{align} tan(\angle DCM) &= \frac{|\overline{DM}|}{|\overline{MC}|} \\
&= \frac{2,5}{2} \,\,\, |tan^{-1}\\
&\Rightarrow \angle DCM = 51,3° \\
\\
\angle ADM &= \angle MCB \\
\\
&\Rightarrow \angle DCB = 2 \cdot 51,3° = 102,6° \\
&\Rightarrow \angle BCD = 360° – 102,6° \end{align}
2.5 Die Bogenlänge kann mit der Formel aus der Formelsammlung berechnet werden. Bestimme dann den Umfang der beschriebenen Figur. Anschließend noch die Prozentrechnung und die Aufgabe ist geschafft.
\begin{align} b &= \frac{\angle DCB}{360°} \cdot 2 \cdot |\overline{CD}| \cdot \pi \\
&= \frac{257,3°}{360°} \cdot 2 \cdot 3,2 \cdot \pi \\
&\Rightarrow b = 14,4 cm \\
\\
u &= b + |\overline{AD}| + |\overline{AB}| \\
&= 14,4 + 7,4 + 7,4 \\
&\Rightarrow u = 29,2 cm \\
\\
p &= \frac{Anteil}{Ganzes} \cdot 100 \% = \frac{14,4}{29,2} \cdot 100\% = 49,3 \% \end{align}
2.6 Manchmal gibt es in der Prüfung zwischendurch auch eine einfache Aufgabe. Nicht misstrauisch werden! Einfach in die Formel einsetzend und fertig. Die Aufgabe ist mit Ergebnissen aus den Aufgaben vorher lösbar. Niemand mitten in der Aufgabe aufgeben, einfach weitermachen. Vielleicht kommt ja noch etwas leichtes!
\begin{align} A_{Sektor} &= \frac{257,3°}{360°} \cdot 3,2^2 \cdot \pi \\
&= 23,0 cm^2 \end{align}
2.7
Achtung, neuer Kreisbogen. Dieser liegt innerhalb des Drachenvierecks. Der Mathe-Lehrer würde sagen, dass es der Kreis über der Strecke \(\overline{BD}\) ist. Das ist der sog. Thaleskreis und alle Punkte auf diesem Kreis bilden mit den Punkten B und D ein rechtwinkliges Dreieck (Grundwissen!). Dabei ist \(\overline{BD}\) die Hypotenuse und die Strecke \(\overline{BE}\) die Ankathete zu den 70°. Damit lässt sich die gesuchte Strecke mit dem Cosinus berechnen.
