Ebene Geometrie – Übung 1

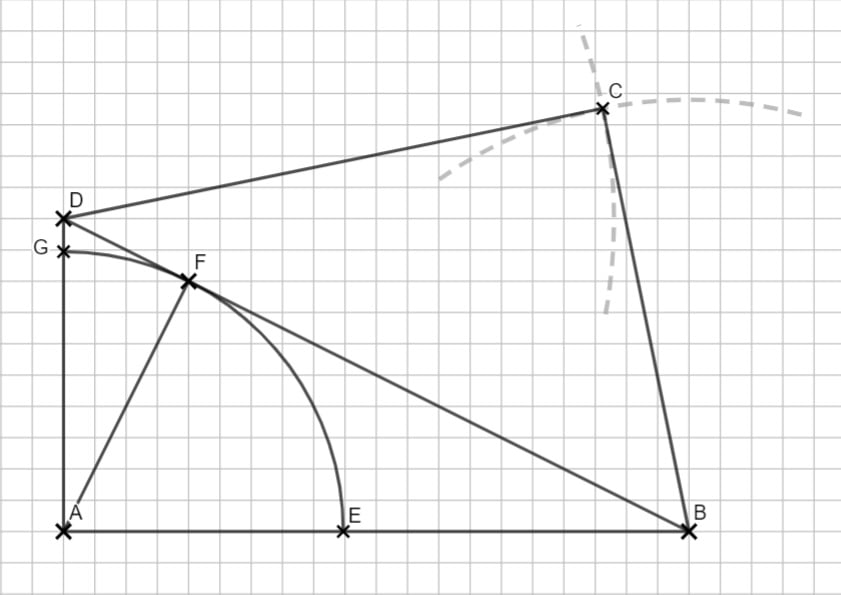
1.1 ink. Kreis. F findest du mit deinem Geodreieck, da hier ein rechter Winkel ist.

1.2 \( |\overline{BD}| \) ist die Hypotenuse im Dreieck ABD. Du kennst beide Katheten, kannst also mit dem Satz des Pythagoras rechnen. Zum gesuchten Winkel kennst du jetzt alle Seiten im Dreieck. Da \( |\overline{AB}| \) und \( |\overline{AD}| \) gegeben ist, rechnest du am Besten damit. Es ist die Gegen- und Ankathete, also benutzt man den Tangens.

\begin{align} |\overline{BD}|^2 &= |\overline{AB}|^2 + |\overline{AD}|^2 \\
|\overline{BD}|^2 &= 10^2 + 5^2 \,\,\, |\sqrt{}\\
&\Rightarrow |\overline{BD}| = 11,2 cm \\
\\
tan(\angle ADB) &= \frac{|\overline{AB}|}{|\overline{AD}|} \\
&= \frac{10}{5} \,\,\, |tan^{-1}\\
&\Rightarrow \angle ADB = 63,4° \end{align}

1.3 Im Dreieck BCD kennst du alle drei Seiten. Du kannst die Umkehrung des Satz des Pythagoras verwenden, also in die Gleichung einsetzen und überprüfen, ob das „=“ erfüllt ist. Wenn das Ist-Gleich stimmt, gibt es einen rechten Winkel gegenüber der längsten Seiten.

\begin{align}|\overline{BD}|^2 &= |\overline{BC}|^2 + |\overline{CD}|^2 \\
11,2^2 &= 6,9^2 + 8,8^2 \,\,\, \text{links und rechts jeweils einzeln ausrechnen}\\
125,4 &= 125,1 \end{align}

Beide Ergebnisse sind sehr nah beieinander und der Unterschied ist durch die Rundung zu erklären. Es gilt also: \( \angle DCB = 90° \)

1.4 Für das allgemeine Viereck gibt es keine Formel. Du zerteilst das Viereck in zwei Dreiecke und weil diese rechtwinklig sind, kannst du mit \( A = 0,5 \cdot \text{Kath} \cdot \text{Kath} \) rechnen.

\begin{align} A_{ABD} &= 0,5 \cdot |\overline{AB}| \cdot |\overline{AD}|\\
&= 0,5 \cdot 10 \cdot 5 \\
&= 25 cm^2\\
A_{BCD} &= 0,5 \cdot |\overline{BC}| \cdot |\overline{CD}|\\
&= 0,5 \cdot 6,9 \cdot 8,8 \\
&= 30,4 cm^2\\
\\
A &= A_{ABD} + A_{BCD} \\
&= 25 + 30,4 \\
&\Rightarrow A = 55,4 cm^2 \end{align}

1.5 Weil der Kreis die Strecke \(\overline{BD}\) im Punkt F berührt, steht der Radius dort senkrecht. Das Dreieck AFD ist also rechtwinklig und du darfst mit Sin/Cos/Tan rechnen.

\begin{align} sin(\angle ADF) &= \frac{|\overline{AF}|}{|\overline{AD}|} \\
sin(63,4°) &= \frac{|\overline{AF}|}{5}\,\,\, |\cdot 5\\
sin(63,4°) \cdot 5 &= |\overline{AF}| \\
&\Rightarrow |\overline{AF}| = r = 4,5 cm \end{align}

1.6 Bei A ist ein rechter Winkel (90°). Mit dem Radius aus 1.5 kannst du den Flächeninhalt bestimmen und anschließend mit dem Ergebnis aus 1.4 die Prozentformel verwenden.

\begin{align} A_{Kreissektor} &= \frac{\alpha}{360°}\cdot |\overline{AF}|^2 \cdot \pi \\
&= \frac{90°}{360°} \cdot 4,5^2 \cdot \pi \\
&A_{Kreissektor} = 15,9 cm^2 \\
\\
p &= \frac{Anteil}{Ganzes} \cdot 100 \% \\
& = \frac{A_{Kreis}}{A_{Viereck}} \cdot 100 \%\\
&= \frac{15,9}{55,4} \cdot 100 \% \\
&\Rightarrow p = 28,7 \% \end{align}

1.7 Dass das Dreieck gleichseitig ist, müssen alle Winkel 90° sein. Es gilt \( |\overline{AF}| = |\overline{EF}| \), weil es beides Radien des Kreises sind. Um den Winkel \( \angle EAF \) zu berechnen, benötigst du du den Winkel \( \angle FAD \) im Dreieck AFD. Dazu verwendet du einfach die Innenwinkelsumme im Dreieck.