Leider ist mir bei der Überarbeitung dieser Aufgabe ein Fehler unterlaufen. Hier <<<Link>>> findest du die ausgebesserte Grafik. Für 2.4 und 2.5 bitte die Aufgabenstellung hier – nicht die gedruckte.
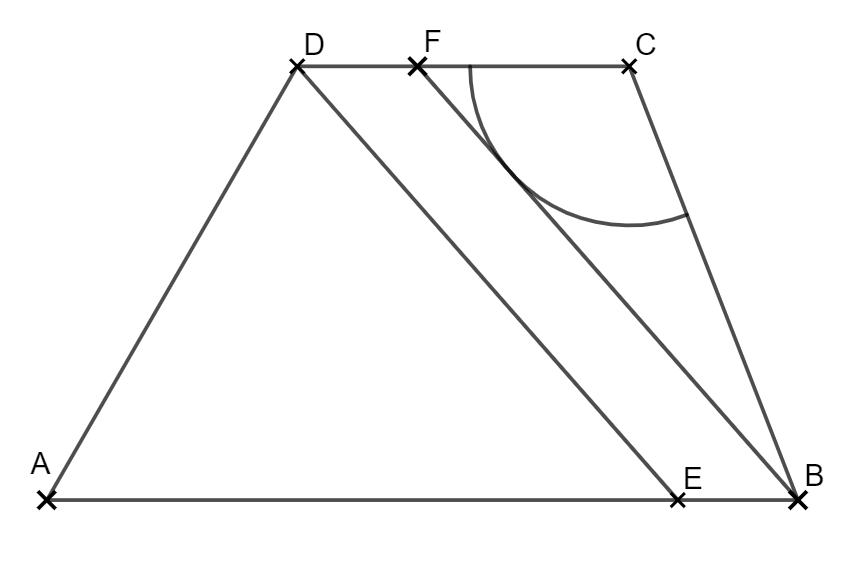
2.0 Die Grundfläche des Erlebnisbeckens eines Schwimmbades hat die Form eines Trapezes mit Kreissektor. Teile des Bodes sollen farbig gestaltet werden. In der Skizze sind die geplanten Bereiche dargestellt.
Es gilt: \( \overline{AB}|| \overline{CD} \, ; \, |\overline{AB}| = 60m \, ; \, |\overline{AC}|= 58m ;\, |\overline{AD}|= 40m ; \angle BAD = 60° \).
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
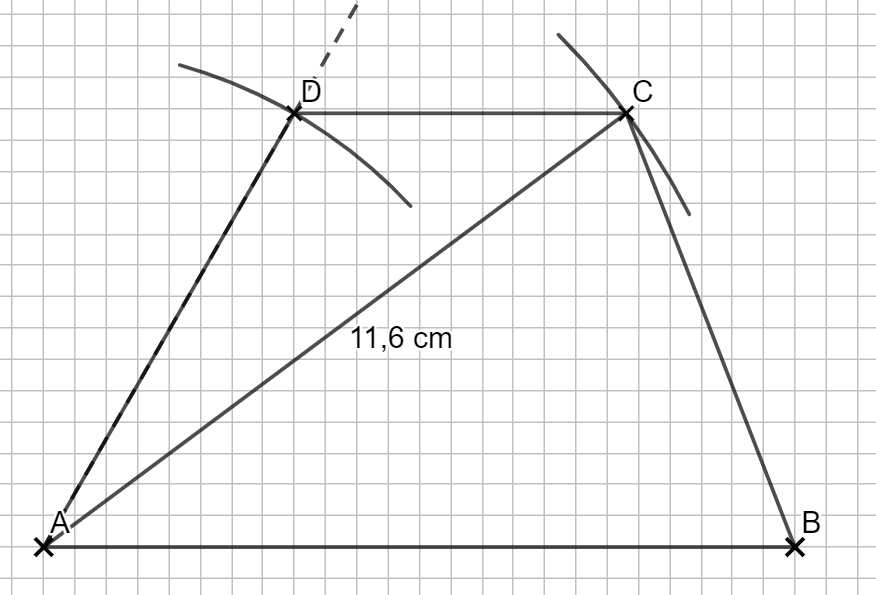
2.1 Zeichnen Sie das Trapez ABCD im Maßstab 1:500.
Lösung zu 2.1
Um die Streckenlängen zu erhalten, in denen du zeichnest, rechnest du zuerst die Meter in Zentimeter um (mal 100) und teilst dann durch den Maßstab (:500).
\begin{align} |\overline{AB}| &= 60m = 6000 cm \Rightarrow 12 cm. \\
|\overline{AC}| &= 11,6 cm \\
|\overline{AD}| &= 8 cm \end{align}
2.2 Berechnen Sie das Maß des Winkels DCA und den Abstand der beiden parallelen Seiten \(\overline{AB}\) und \(\overline{CD}\).
[Ergebnis: \(∢ DCA = 36,67°; d(\overline{AB} ; \overline{CD} ) = 34,64 cm \) ]
Lösung zu 2.2
\begin{align} &\angle DCA \text{ mit dem Sinussatz:}\\
\frac{sin(\angle DCA)}{|\overline{AD}|} &= \frac{sin(\angle ADC)}{|\overline{AC}|} \,\,\, |\cdot |\overline{AD}|\\
sin(\angle DCA) &= \frac{sin(\angle ADC)}{|\overline{AC}|} \cdot |\overline{AD}| \\
&= \frac{sin(180° – 60°)}{58} \cdot 40 \,\,\, |sin^{-1}\\
&\Rightarrow \angle DCA = 36,67° \\
&d(\overline{AB} \, ; \, \overline{CD}) \text{ mit dem Sinus:}\\
sin(\angle BAD) &= \frac{d(\overline{AB} \, ; \, \overline{CD})}{|\overline{AD}} \,\,\, |\cdot |\overline{AD}|\\
&\Rightarrow d(\overline{AB} \, ; \, \overline{CD}) = sin(60°) \cdot 40 = 34,64 m. \end{align}
2.3 Berechnen Sie das Maß des Winkels ACB.
(Ersatzergebnisse: \( |\overline{BC}| = 37,17 m ; ∢ ACB = 74,58° \))
Lösung zu 2.3
Der gesuchte Winkel ACB ist Teil des Dreiecks ABC. Leider hast du hier nur zwei Angaben. Der erste Trick ist nicht ganz einfach zu sehen.
Der Winkel BAC ist ein Weckselwinkel zu DCA und damit 36,67°. Das funktioniert nur, weil AB parallel zu CD ist.
Jetzt hat du drei Angaben im Dreieck ABC, kannst aber den Winkel nicht direkt bestimmen. Zuerst musst du die Streckenlänge \( |\overline{BC}|\) mit dem Cosinussatz bestimmen.
Ja, diesen Weg zu finden ist nicht einfach, so sind diese Aufgaben leider. Wenn du mal nicht weiterkommst, dann achte auf die Zwischenergebnisse. Sie sind ein Hinweis darauf, wie gerechnet werden kann.
\begin{align} &|\overline{BC}| \text{ mit dem Cosinussatz:}\\
|\overline{BC}^2| &= |\overline{AB}|^2 + |\overline{BC}|^2 – 2 \cdot |\overline{AB}| \cdot |\overline{BC}|\cdot cos(\angle BAC) \\
&= 60^2 + 58^2 – 2 \cdot 60 \cdot 58 \cdot cos (36,67°) \,\,\, |\sqrt{} \\
&\Rightarrow |\overline{BC}| = 37,17 \\
\\
&\angle ACB \text{ mit dem Sinussatz:}\\
\frac{sin(\angle ACB)}{|\overline{AB}|}&= \frac{sin(\angle BAC)}{|\overline{BC}|} \,\,\, |\cdot |\overline{AB}|\\
sin(\angle ACB) &= \frac{sin(\angle BAC)}{|\overline{BC}|} \cdot |\overline{AB}|\\
&= \frac{60 \cdot sin(36,67°)}{37,17} \,\,\, |sin^{-1} \\
&\Rightarrow \angle ACB = 74,58° \end{align}
2.4 Durch den trapezförmigen Bereich ABCD des Bodens soll ein blauer Steifen mit den parallelen Begrenzungslinien \( \overline{ED}\) und \(\overline{BF}\) verlaufen. Dabei gilt: E ∈ \(\overline{AB}\) mit ∢ CBF = 20 ° und F ∈ \(\overline{CD} \).
Der kreissektorförmige Bereich mit dem Mittelpunkt C wird in türkiser Farbe gestaltet. Er berührt die Strecke \( \overline{BF} \) im Punkt H.
Zeichnen Sie die Begrenzungslinien \( \overline{ED}\) und \(\overline{BF}\) , sowie den Kreisbogen in die Zeichnung zu 1.1 ein und berechnen Sie die Länge der Strecke \( |\overline{CH}|\).
(Ersatzergebnis: \( |\overline{CH}|\) = 12,71 m)
Lösung zu 2.4
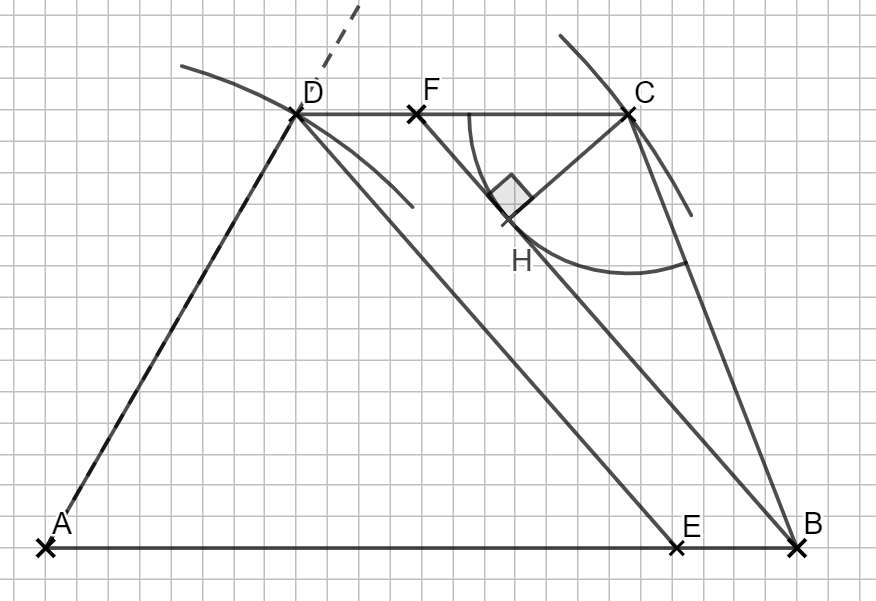
Beim Radius des Kreises kommt die Eigenschaft mit dem Berührpunkt ins Spiel. \( \overline{CH} \) steht senkrecht, weil H ein Berührpunkt ist.
Du kennst aus der Aufgabenstellung den Winkel bei B und zusammen mit der Streckenlänge \( |\overline{BC}|\) kannst du mit dem Sinus ansetzen.
\begin{align} &r = |\overline{CH}| \text{ mit dem Sinus:}\\
sin(\angle CBF) &= \frac{|\overline{CH}|}{|\overline{BC}|} \,\,\, |\cdot |\overline{BC}| \\
|\overline{CH}| &= sin(\angle CBF) \cdot |\overline{BC}| \\
&= sin(20°) \cdot 37,17 m \\
&\Rightarrow |\overline{CH}| = 12,71 m \end{align}
2.5 Berechnen Sie die benötigte Menge blaue und türkise Farbe, wenn pro Quadratmeter 0,18 l benötigt werden. Entnehmen Sie hierzu die die Länge \( |\overline{BE}|\) aus der Zeichnung.
Lösung zu 2.5
Für die Flächenformel des Kreissektors benötigst du den Innenwinkel, den du leicht durch Addition von DCA und ACB bekommst.
Der Flächeninhalt des Parallelgramms berechnet sich durch \( A = g \cdot h \). Hier ist die Grundseite \( \overline{BE} \) und die Höhe \( d(\overline{AB} \, ; \, \overline{CD}) \) kennst du schon aus 1.2.
Die Grundseite darfst du messen. Es sind 1,9 cm, was mit 500 multipliert und durch 100 geteilt 9,5 m ergibt.
Jetzt musst du nurnoch einsetzen.
\begin{align} &A_{Sektor} \text{ mit der Flächenformel:}\\
A_{Sektor} &= \frac{\angle DCB}{360°} \cdot |\overline{CH}|^2 \cdot \pi \\
&= \frac{111,25°}{360°} \cdot 12,71^2 \cdot \pi \\
&\Rightarrow A_{Sektor} = 156,83 m^2 \\
&\Rightarrow V_1 = A_{Sektor} \cdot 0,18 = 28,23 l \\
\\
A_{Parallelogramm} &= |\overline{BE}| \cdot d(\overline{AB} \, ; \, \overline{CD}) \\
&= 9,5 \cdot 34,64 \\
&\Rightarrow A_{Parallelogramm} = 329,08 m^2 \\
&\Rightarrow V_2 = A_{Parallelogramm} \cdot 0,18 = 59,23 l \end{align}