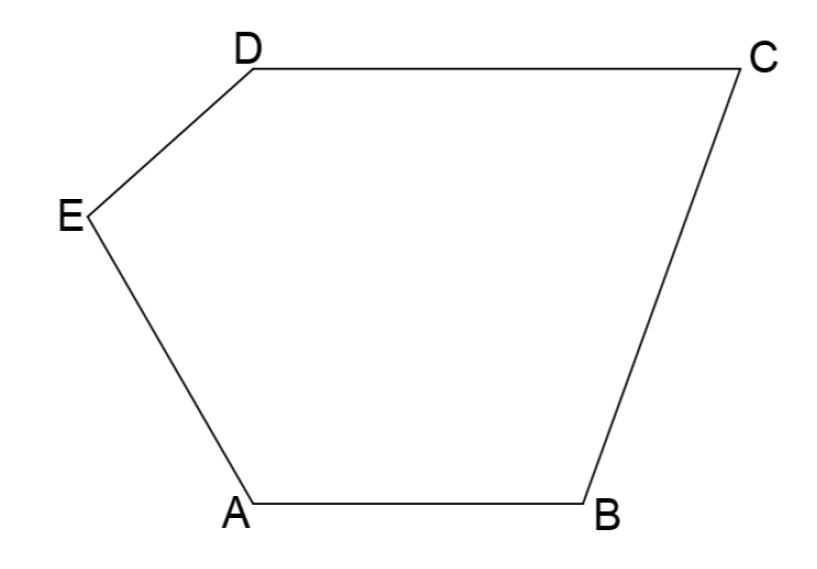
1.0 Gegeben ist ein Fünfeck ABCDE mit folgenden Angaben:
\(|\overline{AB}| = 5 cm; |\overline{BC}| = 7 cm; |\overline{AE}| = 5 cm; \angle CBA = 110°; \angle BAE = 120°. \)
Es gilt: \( \overline{AB}\, || \, \overline{CD} ; \overline{AD} \, \perp \, \overline{AB} \).
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
1.1 Zeichnen Sie das Fünfeck ABCDE.
Lösung zu 1.1
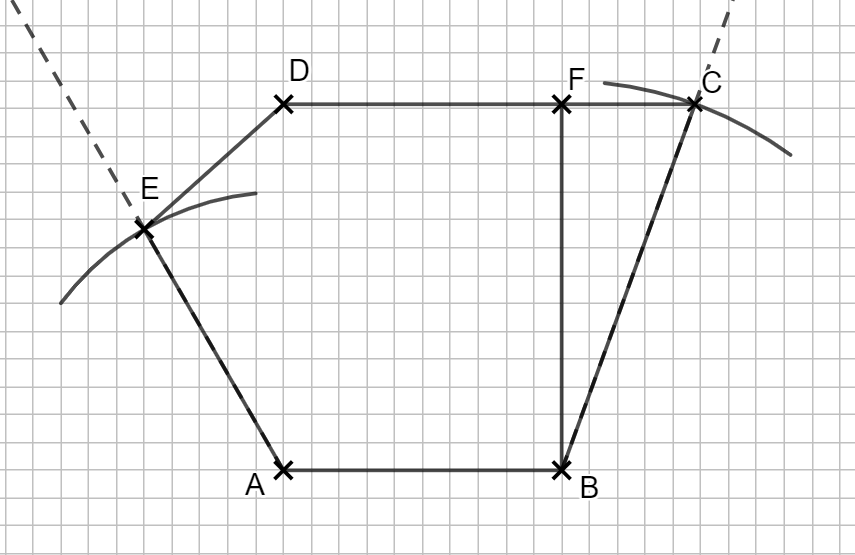
1.2 Sei F der Lotfußpunkt von B zur Strecke \(\overline{CD} \). Zeichnen Sie F und die Strecke \(\overline{BF} \) in die Zeichnung zu 1.1 ein und berechnen Sie sodann deren Länge
[Teilergebnis: \( |\overline{BF}| = 6,58 cm \)]
Lösung zu 1.2
\begin{align} &\text{Berechnung von: } |\overline{BF}| \text{ mit dem Cosinus:}\\
cos(\angle CBF) &= \frac{|\overline{BF}|}{|\overline{BC}|} \\
cos(110° – 90°) &= \frac{|\overline{BF}|}{7} \,\,\, |\cdot 7 \\
&\Rightarrow |\overline{BF}| = cos(20°) \cdot 7 = 6,58 \text{cm}\end{align}
1.3 Bestimmen Sie das Maß des Winkels ∢AED.
[Ergebnis: \( |\overline{ED}| = 3,36 cm; \angle AED = 102,04° \) <- dieses Ersatzergebnis ist falsch! Bitte für das richtige Ergebnis in die Lösung schauen.]
Lösung zu 1.3
Im Dreieck AED hast du zwar drei Angaben, aber leider kannst du den Winkel bei E nicht direkt berechnen. Zuerst musst du über einen Zwischenschritt die Streckenlänge \( |\overline{ED}|\) bestimmen.
Diese Streckenlänge ist auch als Zwischenergebnis angegeben. Die Aufgabe verrät dir also den Lösungsweg.
\begin{align} &|\overline{ED}| \text{ mit dem Cosinussatz:}\\
|\overline{ED}|^2 &= |\overline{AE}|^2 + |\overline{AD}|^2 – 2 \cdot |\overline{AE}| \cdot |\overline{AD}| \cdot cos(\angle EAD) \\
&= 5^2 + 6,58^2 – 2 \cdot 5 \cdot 6,58 \cdot cos(120° – 90°) \,\,\, |\sqrt{}\\
&\Rightarrow |\overline{ED}| = 3,36 \text{cm} \\
\\
&\angle AED \text{ mit dem umgeformten Cosinussatz:}\\
cos(\angle AED) &= \frac{|\overline{AE}|^2 + |\overline{ED}|^2 – |\overline{AD}|^2|}{2 \cdot |\overline{AE}| \cdot |\overline{ED}|} \\
&= \frac{5^2 + 3,36^2 – 6,58^2}{2 \cdot 5 \cdot 3,36} \,\,\, |cos^{-1}\\
\Rightarrow &\angle AED = 102,04 ° \end{align}
Achtung: Verwendet man hier den Sinussatz, dann tritt der Spezialfall mit Winkel größer als 90° auf und man muss bedenken, dass das wahre Ergebnis nicht 78,28° ist, sondern 180° – 78,28°. Oder einfach lieber den Cosinussatz verwenden.
1.4 Berechnen Sie den Flächeninhalt des Fünfecks ABCDE.
Lösung zu 1.4
Das Fünfeck setzt sich aus dem Dreieck ADE, dem Rechteck ABFD und dem Dreieck BCF zusammen. Du berechnest die einzelnen Teilflächen und addierst dann.
\begin{align}
A_{ADE} &= 0,5 \cdot |\overline{AE}| \cdot |\overline{AD}| \cdot sin(\angle DAE) \\
&= 0,5 \cdot 5 \cdot 6,58 \cdot sin(30°) \\
&\Rightarrow A_{ADE} = 8,23 \text{cm}^2 \\
\\
A_{ABFD} &= |\overline{AB}| \cdot |\overline{AD}| \\
&= 5 \cdot 6,58 \\
&\Rightarrow A_{ABFD} = 32,9 \text{cm}^2 \\
\\
A_{BCF} &= 0,5 \cdot |\overline{BC}| \cdot |\overline{BF}| \cdot sin(\angle CBF) \\
&= 0,5 \cdot 7 \cdot 6,58 \cdot sin(20°) \\
&\Rightarrow A_{BC} = 7,88 \text{cm}^2 \\
\\
A_{ABCDE} &= A_{ADE} + A_{ABFD} + A_{BCF} \\
&= 8,23 + 32,9 + 7,88 \\
&\Rightarrow A_{ABCDE} = 49,01 \text{cm}^2 \end{align}
1.5 Ein Kreisbogen um E berührt die Strecke \(\overline{AD} \) im Punkt G. Zeichnen Sie den Kreisbogen in die Zeichnung zu 1.1 ein und berechnen Sie seinen Flächeninhalt des Kreissektors.
Lösung zu 1.5
Einzeichnen des Kreisbogens
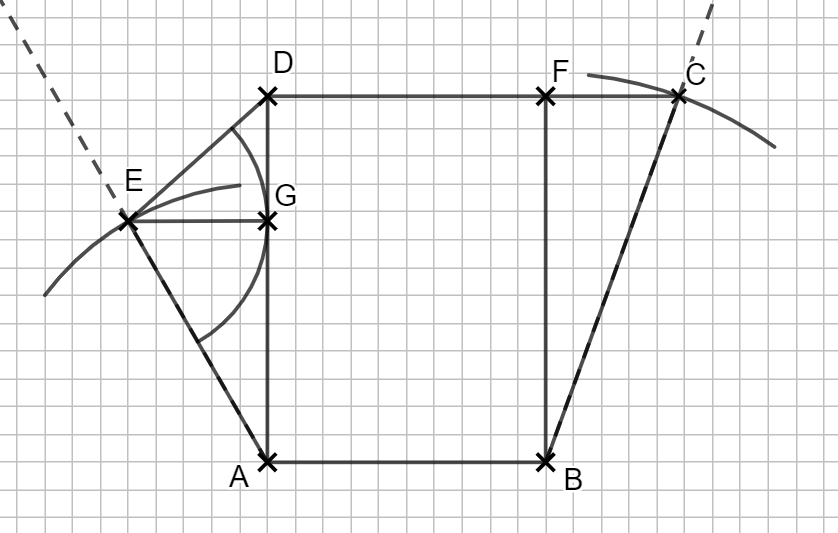
Strecke \( \overline{AD}\) berührt, steht der Radius senkrecht auf dieser Strecke. Du kannst im Dreieck AGE also mit Sinus, Cosinus, Tangens und dem Satz des Pythagoras rechnen.
\begin{align} &|\overline{EG}| \text{ mit dem Sinus:}\\
sin(\angle DAE) &= \frac{|\overline{EG}|}{|\overline{AE}|} \\
sin(30°) &= \frac{|\overline{EG}|}{5} \,\,\, |\cdot 5 \\
&\Rightarrow |\overline{EG}| = sin(30°) \cdot 5 = 2,5 \text{cm}\\
\\
&\text{Berechnung des Flächeninhalts:}\\
A &= \frac{\angle AED}{360°} \cdot |\overline{EG}|^2 \cdot \pi \\
&= \frac{102,04°}{360°} \cdot 2,5^2 \cdot \pi \\
&\Rightarrow A = 5,57 \text{ cm}^2 \end{align}