1.0 Hanna hat sich für die Schule einen Farbwürfel gekauft, der auf zwei Feldern die Farbe Grün und auf vier Feldern die Farbe Rot hat. Bei Überschriften würfelt sie für jedes Wort einzeln die Farbe aus, in der sie dieses dann schreibt.
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
1.1 Bestimmen Sie die Anzahl an Kombinationsmöglichkeiten die Überschrift „Daten und Zufall“ in verschiedenen Farben zu schreiben.
Lösung zu 1.1
Insgesamt gibt es 8 Möglichkeiten, denn für jedes der drei Wörter gibt es zwei verschiedene Farben. Die Überschrift darf aber nicht einfarbig, also Grün-Grün-Grün bzw Rot-Rot-Rot sein. Es fallen zwei Möglichkeiten weg.
Es gibt 6 Kombinationsmöglichkeiten.
1.2 Zeichnen Sie ein Baumdiagramm für Überschriften mit drei Wörtern, in dem die Wahrscheinlichkeiten in Brüchen ersichtlich werden.
Lösung zu 1.2
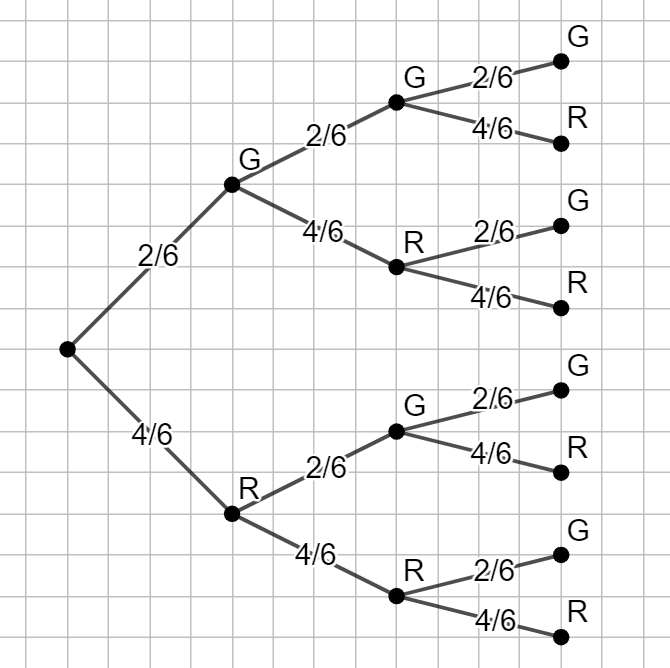
1.3 Berechnen Sie die Chance als Bruch, dass nur das erste Wort rot ist.
Lösung zu 1.3
Die Aufgabe beschreibt in kompliziert das Ereignis P(rot, grün, grün).
\begin{align} P(R,G,G) &= P(R) \cdot P(G) \cdot P(G) \\
&= \frac{4}{6} \cdot \frac{2}{6} \cdot \frac{2}{6} \\
&= \frac{2}{3} \cdot \frac{1}{3} \cdot \frac{1}{3} \\
&\Rightarrow P(R,G,G) = \frac{2}{27} \end{align}
Nebenrechnung: 200 : 27 = 0,074…
\( \frac{2}{27} = 0,074 \approx 7 \% \)
1.4 Berechnen Sie die Chance, dass Hanna eine einfarbige Überschrift schreibt.
Lösung zu 1.4
Das Ereignis setzt sich aus P(R,R,R) und P(G,G,G) zusammen. Diese berechnest du einzeln und addierst anschließend.
\begin{align} P(R,R,R) &= P(R) \cdot P(R) \cdot P(R) \\
&= \frac{4}{6} \cdot \frac{4}{6} \cdot \frac{4}{6} \\
&= \frac{2}{3} \cdot \frac{2}{3} \cdot \frac{2}{3} \\
&\Rightarrow P(R,R,R) = \frac{8}{27}\\
\\
P(G,G,G) &= P(G) \cdot P(G) \cdot (G) \\
&= \frac{2}{6} \cdot \frac{2}{6} \cdot \frac{2}{6} \\
&= \frac{1}{3} \cdot \frac{1}{3} \cdot \frac{1}{3} \\
&\Rightarrow P(G,G,G) = \frac{1}{27} \\
\\
P_{ges} &= P(R,R,R) + P(G,G,G) \\
&= \frac{8}{27} + \frac{1}{27} \\
&= \frac{9}{27} \\
&\Rightarrow P_{ges} = \frac{1}{3} \approx 33 \% \end{align}
