Lösung zu 1
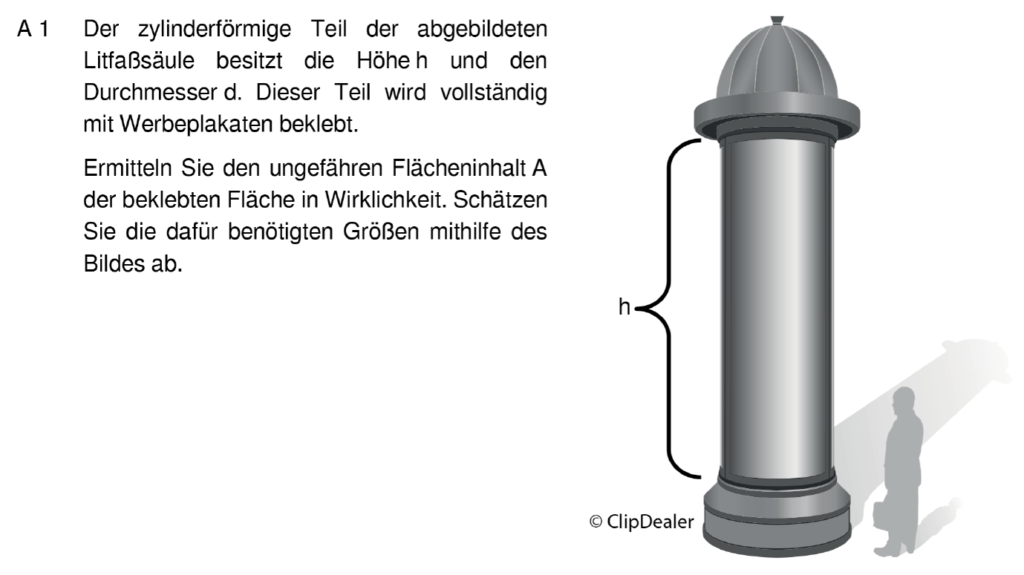
Wir schätzen den Mann auf 1,8 m. Mit Hilfe des Geodreiecks kannst du schätzen, dass der Mann 2x in die Höhe der Werbefläche passt. Der Durchmesser ist etwas größer als die Hälfte seiner Höhe, also ~1 Meter.
\begin{align}
A_{Mantelfläche} &= d \cdot \pi \cdot h\\
&= 1 \cdot \pi \cdot 3,6 \\
&= 3,6 \cdot \pi \\
&= 3,6 \cdot 3,14 \,\,\, \text{einen größer, einen kleiner „runden“}\\
&= 3,5 \cdot 3 \\
A = 10,5 m² \end{align}
Niemand weiß, welche Genauigkeit bei der Schätzung erlaubt ist. Das offizielle Lösungsmuster rundet z.B. 3,6 auf 4 auf und erhält einen Flächeninhalt von 12 m². Am Ende muss deine Abschätzung irgendwie sinnvoll sein. Abschätzen „mit der Axt“ scheint erlaubt zu sein.
Meine persönliche Meinung: Wenn man die Höhe auf 3,6 schätzt ist es nicht clever auf 4 Meter zu runden, denn wenn das Werbebanner oben und unten übersteht, muss es unpraktisch abgeschnitten werden. Die Werbung überlappend einmal außenrum zu kleben ist dagegen sehr einfach. Aber mei … wir sind hier in der Mathematik, da interessiert die Praxis nicht 😉
