

Lösung zu B4.1
Die Diagonalen stehen in einem Drachenviereck senkrecht, du darfst sie also im 45°-Winkel in halber Länge nach vorne und nach hinten zeichnen.
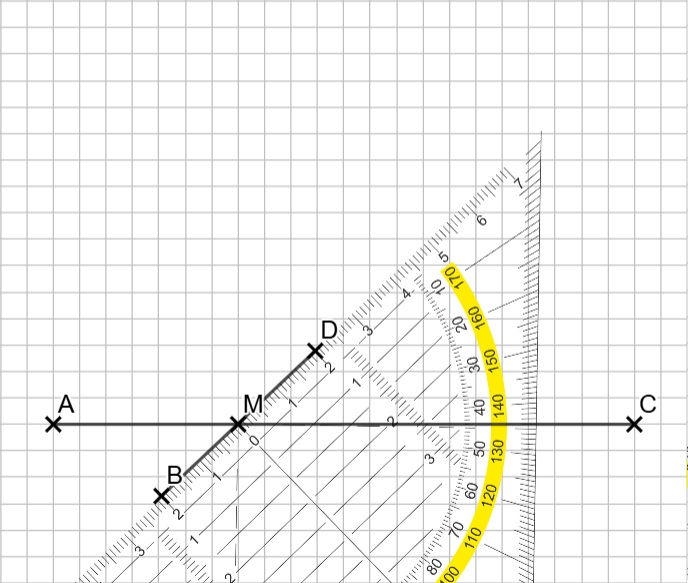
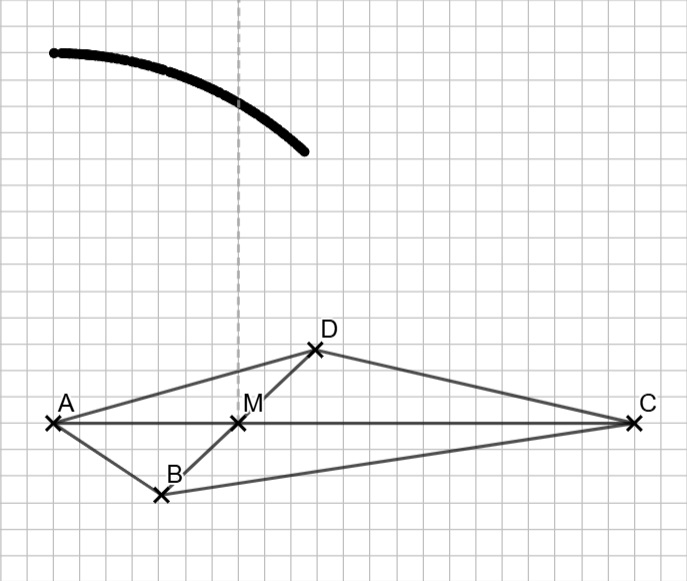
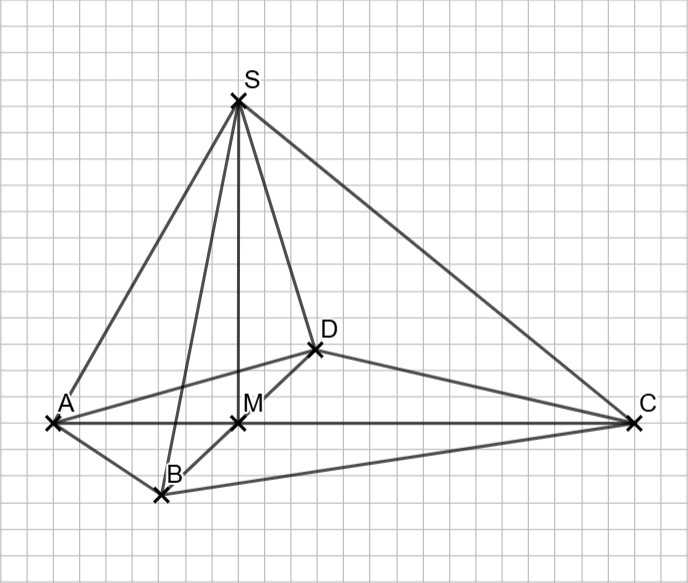
Hier geht es zur allgemeinen Erklärung:

Lösung zu B4.2
Die Höhe steht immer senkrecht. Versuche es also mal mit Sinus/Cosinus/Tangens oder Satz des Pythagoras
Die Höhe steht in der Pyramide senkrecht, also kannst du mit Sin/Cos/Tan und des mSatz des Pythagoras rechnen. Ich rechne hier zuerst die Höhe aus, um dann mit dem Satz des Pythagoras weitermachen zu können, aber du könntest auch in der Reihenfolge der Aufgabe arbeiten, indem du den Cosinussatz für \( \overline{CS}\) verwendest
\begin{align} &\angle CAS \text{ mit dem Cosinus im Dreieck AMS}\\
cos(\angle CAS) &= \frac{|\overline{AM}|}{|\overline{AS}|} \\
cos(\angle CAS) &= \frac{3,5}{7} \,\,\,|cos^{-1}\\
\Rightarrow &\angle CAS = 60° \\
\\
&|\overline{MS}| \text{ mit dem Satz des Pythagoras im Dreieck AMS:}\\
|\overline{MS}|^2 &= |\overline{AS}|^2 – |\overline{AM}|^2 \\
&= 7^2 – 3,5^2 \,\,\, |\sqrt{}\\
\Rightarrow &|\overline{MS}| = 6,06 cm \\
\\
& |\overline{CS}| \text{ mit dem Satz des Pythagoras im Dreieck MCS:}\\
|\overline{CS}|^2 &= |\overline{MC}|^2 + |\overline{MS}|^2 \\
&= 7,5^2 + 6,06^2 \,\,\, |\sqrt{}\\
\Rightarrow &|\overline{CS}| = 9,64 cm \end{align}
Hier geht es zur allgemeinen Erklärung:

Lösung zu B4.3
Überlege dir, wann das größte Dreieck entsteht und berechne seinen Flächeninhalt. Wenn das größte Dreieck kleiner als 35cm² ist, kann es kein Dreieck mit 35 cm² geben.
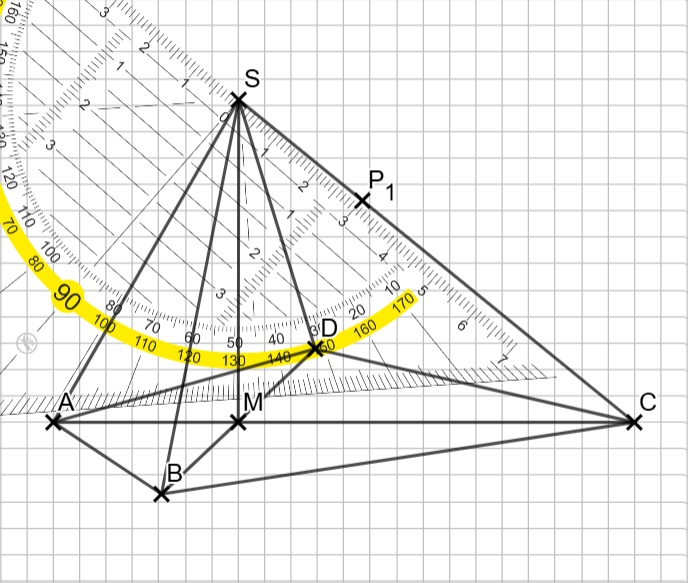
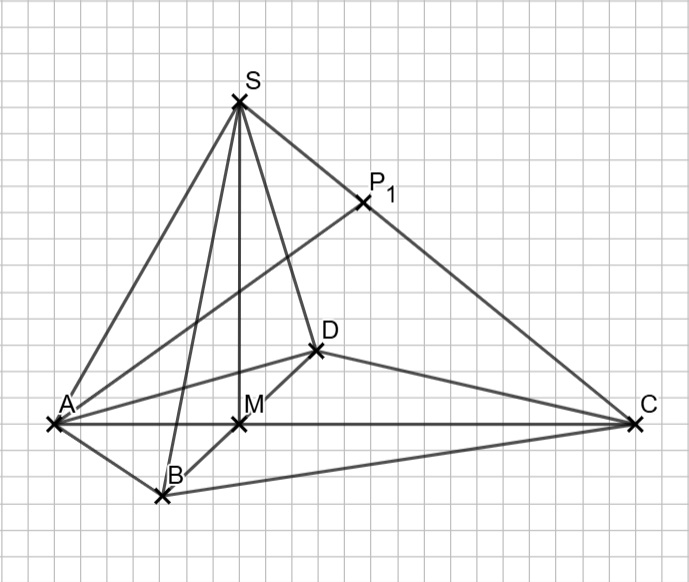
Das größte Dreieck entsteht, wenn P auf C liegt. In diesem Fall ist das Dreieck die „ganze Fläche“, die du in der Pyramide siehst. Jedes Dreieck ist kleiner als dieses Dreieck mit P auf C. Den Flächeninhalt dieses Dreiecks kannst du leicht aus den Angaben besteimmen:
\begin{align} A &= 0,5 \cdot g \cdot h \\
&= 0,5 \cdot |\overline{AC}| \cdot |\overline{MS}| \\
&= 0,5 \cdot 11 \cdot 6,06 \\
\Rightarrow &A = 33,33 cm^2 \end{align}
Weil jedes Dreieck einen kleineren Flächeninhalt als 33,33 cm² hat, kann es keines mit 35 cm² geben.
Hier geht es zur allgemeinen Erklärung:

Lösung zu B4.4
Eine Strecke mit minimaler Länge ist hier der Abstand. Ein rechter Winkel hilft dir also beim Einzeichnen und bei der Rechnung.
Das Stichwort minimale Länge sagt dir, dass diese Strecke senkrecht steht. Weil ein rechtwinkliges Dreieck entsteht, kannst du Sin/Cos/Tan und den Satz des Pythagoras zur Berechnung verwenden.
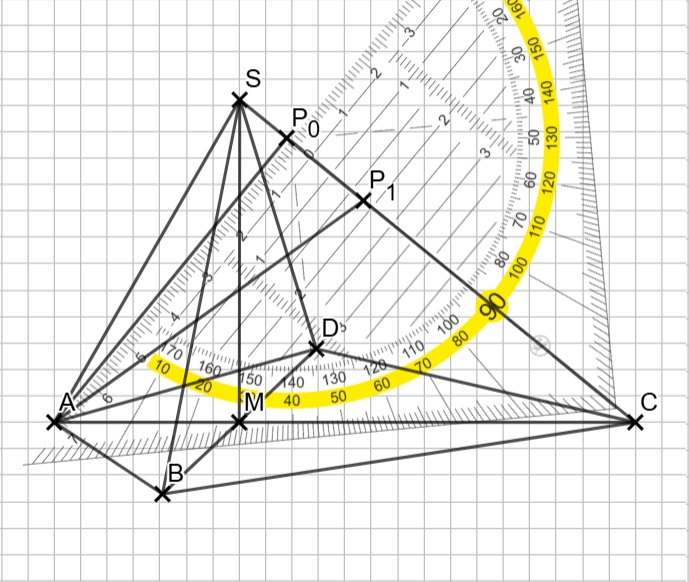
Um rechnen zu können, brauchst du den Winkel bei C, den man in einem kurzen Zwischenschritt bestimmt.
\begin{align} &\angle SCA \text{mit dem Cosinus im Dreieck MCS:}\\
cos(\angle SCA) &= \frac{|\overline{CM}|}{|\overline{CS}|} \\
cos(\angle SCA) &= \frac{7,5}{9,64} \,\,\, |cos^{-1}\\
\angle SCA &= 38,92° \\
\\
&|\overline{AP_0}| \text{mit dem Sinus im Dreieck ACP:}\\
sin(\angle SCA) &= \frac{|\overline{AP_0}|}{|\overline{AC}|}\\
sin(38,92°) &= \frac{|\overline{AP_0}|}{11} \,\,\, |\cdot 11\\
\Rightarrow &|\overline{AP_0}| = 6,91 cm \end{align}
Hier geht es zur allgemeinen Erklärung:

Lösung zu B4.5
In der Formel zur Pyramide ist dir bestimmt klar, dass die Grundfläche hier immer gleich ist (ohne x), sich die Höhe aber verändert (mit x). Berechne die beiden Bausteine einzeln und setze dann in die Formel ein.
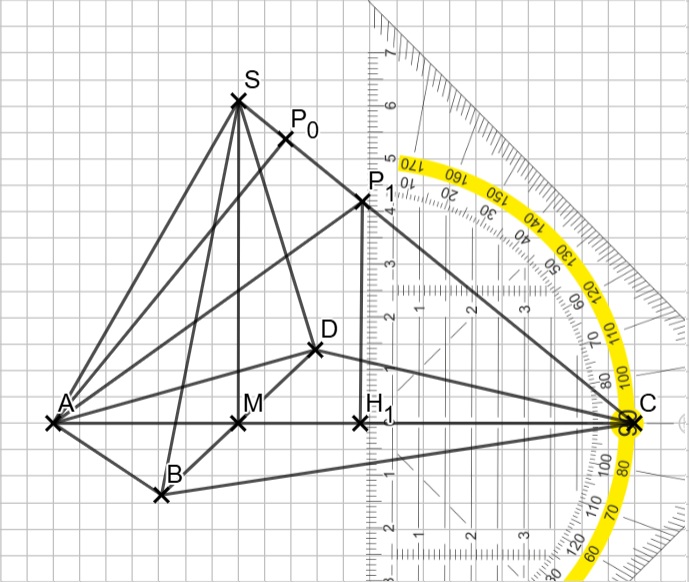
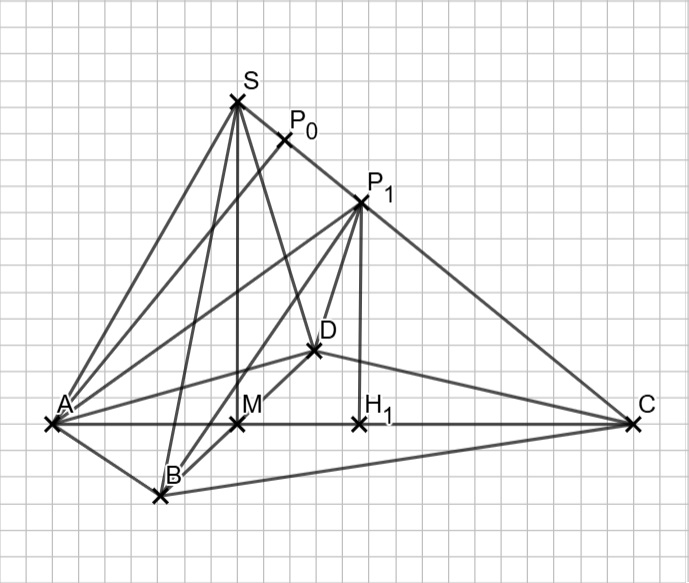
\begin{align} A_g &= \frac{1}{2} \cdot |\overline{AC}| \cdot |\overline{BD}| \\
&= \frac{1}{2} \cdot 11 \cdot 8 \\
&= 44 cm ^2 \\
\\
&h = |\overline{H_n P_n}| \text{ mit dem Vierstreckensatz:}\\
\frac{h}{|\overline{MS}|} &= \frac{|\overline{CP_n}|}{|\overline{CS}|} \\
\frac{h}{6,06} &= \frac{9,64 – x}{9,64} \,\,\, |\cdot 6,06\\
h &= \frac{9,64 – x}{9,64} \cdot 6,06 \,\,\, |\text{Bruch aufteilen}\\
h &= (\frac{9,64}{9,64} – \frac{x} {9,64}) \cdot 6,06 \,\,\, |\text{ Ersten Bruch kürzen}\\
h &= (1 – \frac{x}{9,64})\cdot 6,06 \,\,\, |\text{ 6,06 in die Klammer multiplizeren}\\
h &= 1 \cdot 6,06 – \frac{x}{9,64} \cdot 6,06 \text{ Jeweils die Zahlen verrechnen}\\
h &= 6,06 – 0,63x \\
\\
&\text{Einsetzen in die Volumenformel:}\\
V &= \frac{1}{3} \cdot A_g \cdot h \\
&= \frac{1}{3} \cdot 44 \cdot (6,06 – 0,63x) \,\,\, |\frac{44}{3} \text{ in die Klammer multiplizieren}\\
\Rightarrow &V = (88,88 – 9,24x) cm^3 \end{align}

Lösung zu B4.6
Für die vorgegebene Höhe von 4 kannst du das entsprechende Volumen bestimmen. Das ist das „Ergebnis“, das die Formel aus 4.5 ergeben soll.
Berechne das Volumen für h = 4. Setzt du das Ergebnis mit der Formel aus 4.5 gleich, erhältst du eine Gleichung, die du nach x auflösen kannst.
\begin{align} V(h=4) &= \frac{1}{3} \cdot 44 \cdot 4 = 58,67 cm^3\\
\\
V(x) = 58,67 \\
88,88 – 9,24x &= 58,67 \,\,\, |-88,88 \\
-9,24x &= -30,21 \,\,\,|:(-9,24) \\
\Rightarrow &x = 3,27 \end{align}
