

Lösung zu B3.1
Du hast zwei Punkte, also musst du zwei Gleichungen aufschreiben und das Gleichungssystem lösen
Stelle ein Gleichungssystem auf, indem du in die Parabelgleichung jeweils einen Punkt einsetzt.
\begin{align} &\text{ Gleichungsystem aus P und Q:}\\
(I) y &= -0,4 x^2 +bx +c \,\,\, | \text{mit } P(-5|-14) \\
(I) -14 &= -0,4 \cdot (-5)^2 + b \cdot (-5) + c \\
(I) -14 &= -10 -5b + c \,\,\, |+10 \\
(I) -4 &= -5b + c \\
\\
(II) y &= -0,4 x^2 +bx +c \,\,\, | \text{mit } Q(-1|2) \\
(II) 2 &= -0,4\cdot (-1)^2 +b \cdot (-1) + c \\
(II) 2 &= -0,4 – b + c \,\,\, |+0,4 \\
(II) 2,4 &= -b + c \\
\\
\Rightarrow & TR \Rightarrow Mode A \Rightarrow 1 \Rightarrow 2 \\
\\
&b = 1,6 \, ; \, c = 4 \end{align}
Gib den Parabelterm in den Taschenrechner ein und lass dir eine Tabelle ausgeben. Die Punkte eintragen und mit einer Freihandlinie verbinden.
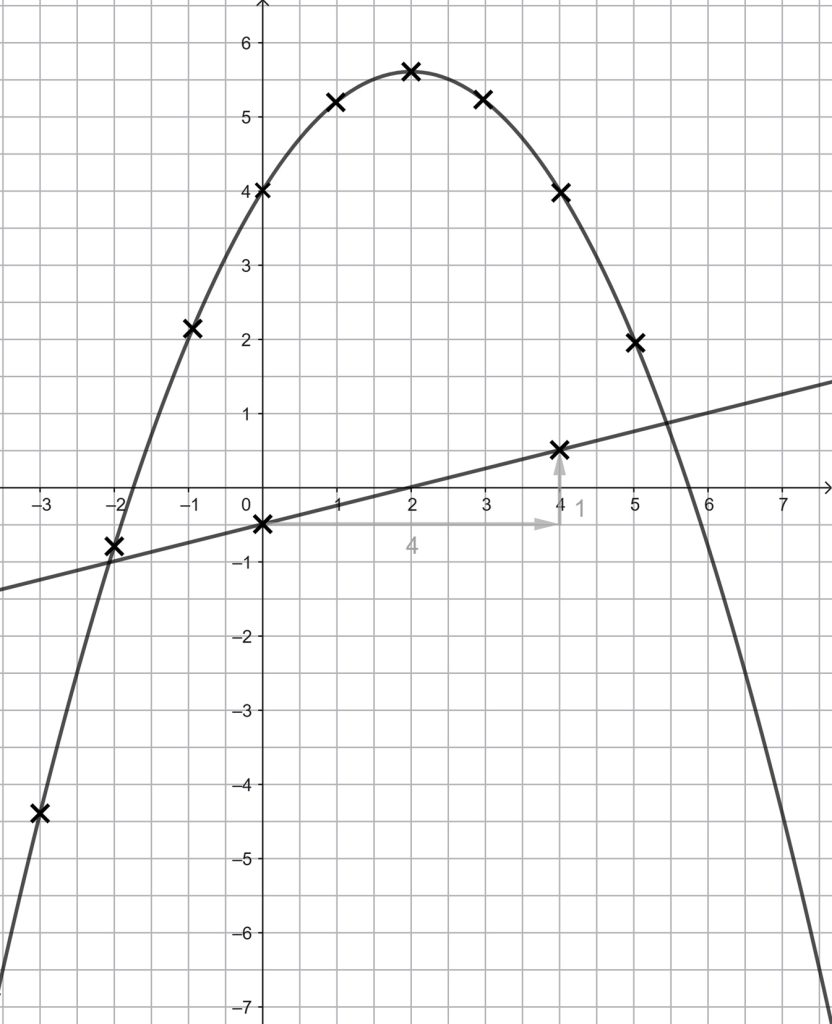
Hier geht es zur allgemeinen Erklärung:

Lösung zu B3.2
Gleichschenklige Dreiecke sind achsensymmetrisch, also „links und rechts gleich“.
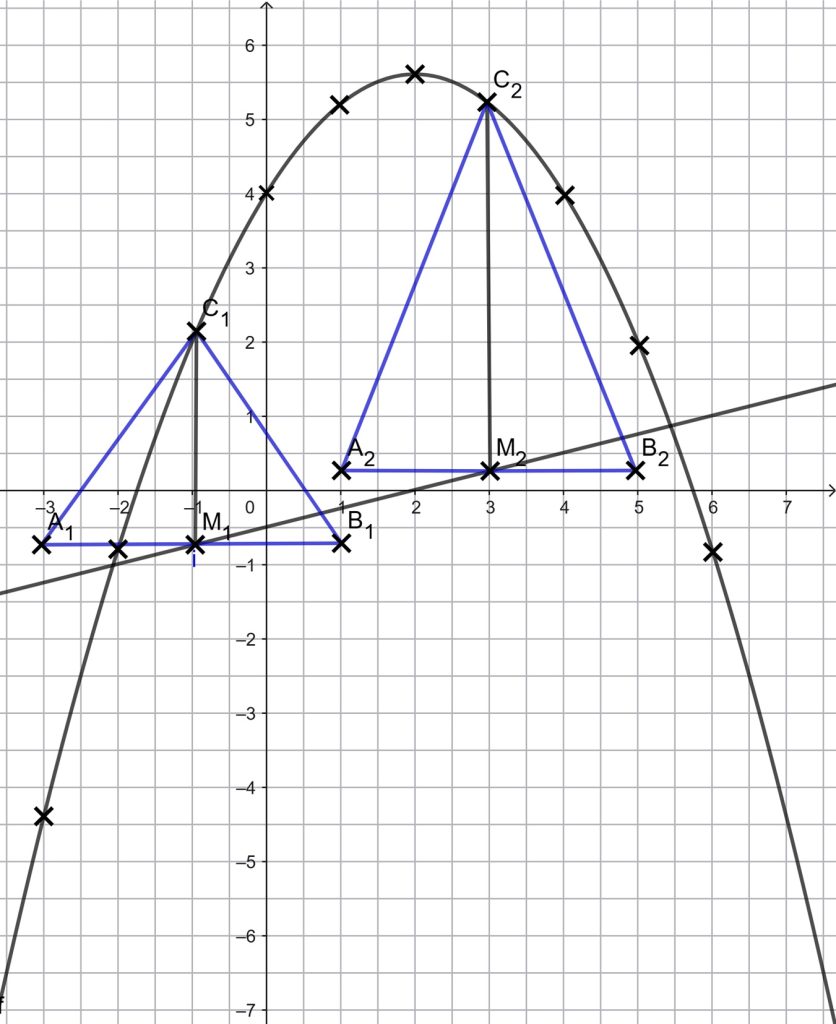
Hier geht es zur allgemeinen Erklärung:

Lösung zu B3.3
Berechne die funktionale Länge durch „oben – unten“. Schau dazu nochmal ins Koordinatensystem, welche Funktion oben ist. In der zweiten Hälfte brauchst du nur deinen Taschenrechner.
\begin{align} |\overline{C_nM_n}|(x) &= „oben – unten“ \\
&= -0,4x^2 +1,6x +4 – (0,25x – 0,5)\\
&= -0,4x^2 +1,6x +4 – 0,25x + 0,5 \\
&= -0,4x^2 +1,35x + 4,5 \\
\\
\Rightarrow &TR \Rightarrow Mode A \Rightarrow 2 \Rightarrow 2 \\
&|\overline{C_0M_0}| = 5,64 cm \, \text{ für } \, x = 1,69 \end{align}
Hier geht es zur allgemeinen Erklärung:

Lösung zu B3.4
Mache dir eine Skizze, wie das gesuchte Dreieck aussieht und überlege dir daran, was du alles darüber weißt.
Dass bei C ein 90°-Winkel entsteht, muss der Winkel in zwei 45° Winkel halbiert werden. Der Winkel ACM muss dann z.B. 45° sein.
Dort entstehen 45°, wenn wenn das Dreieck gleichschenklig ist, also \( |\overline{AM}| = |\overline{CM}| \) gilt.
Da \( |\overline{AM}| = 2 cm \) laut der Aufgabenstellung gilt, muss auch \( |\overline{CM}| = 2cm \) gelten. Für die Fläche ergibt sich dann:
Hier geht es zur allgemeinen Erklärung:

Lösung zu B3.5
In diesen Dreiecken sind alle Seiten gleich-lang und du weißt etwas über eine Seite. Schau mal in 3.2 nach! Skizzen helfen für die kommenden Rechnungen!
Das Dreieck ist gleichseitig, wenn alle Seiten gleich lang sind. Soweit so klar.
Die Basis \( |\overline{AB}| = 4 \) ist festgelegt, also kann nur ein
gleichseitiges Dreieck entstehen, wenn alle Seiten 4 LE lang sind.
Die Höhe des Dreiecks kann also mit dem Satz des Pythagoras ausgerechnet werden.
\begin{align} |\overline{AC}|^2 &= |\overline{AM}|^2 + |\overline{CM}|^2 \,\,\, | – |\overline{AM}|^2 \\
|\overline{CM}|^2 &= |\overline{AC}|^2 – |\overline{AM}|^2 \\
&= 4^2 – 2^2 \,\,\, |\sqrt{}\\
&\Rightarrow |\overline{CM}| = 3,46 \end{align}
Diesen Zahlenwert kann du jetzt mit der Formel aus 3.4 gleichsetzen und so an das x kommen.
\begin{align} |\overline{C_nM_n}|(x) &= 3,46 \\
-0,4x^2 +1,35x + 4,5 &= 3,46 \,\,\, |-3,46 \\
-0,4x^2 + 1,35x + 1,04 &= 0 \\
\\
\Rightarrow &TR \Rightarrow Mode A \Rightarrow 2 \Rightarrow 2 \\
x_1 = 4,02 \, &; \, x_2 = -0,65 \end{align}
Hier geht es zur allgemeinen Erklärung:
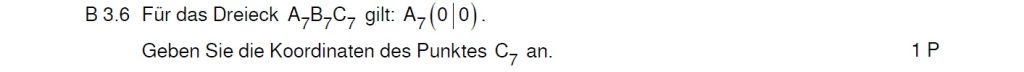
Lösung zu B3.6
Du kannst dir anhand der Eigenschaften des Dreiecks in dieser Aufgabe einen Weg über den Mittelpunkt der Basis und dann nach oben überlegen.
Wenn A im Ursprung liegt, dann liegt der Mittelpunkt M zwei Längeneinheiten weiter rechts, also bei M(2|0). Denn das ist ja immer gleich.
Mit der Formel aus 3.4 kannst du die Höhe für einen Wert von x berechnen. Und das ist hier die 2.
\begin{align} |\overline{C_nM_n}|(x) &= -0,4x^2 +1,35x + 4,5 \\
|\overline{C_nM_n}|(2) &= -0,4\cdot 2^2 + 1,35\cdot 2 + 4,5 \\
&= 5,6 \end{align}
Diesen Wert schieben wir das M nach oben – also entlang der y-Kooridnate – und landen bei C.
\( M_7(2|0) \Rightarrow C_7(2|5,6) \)