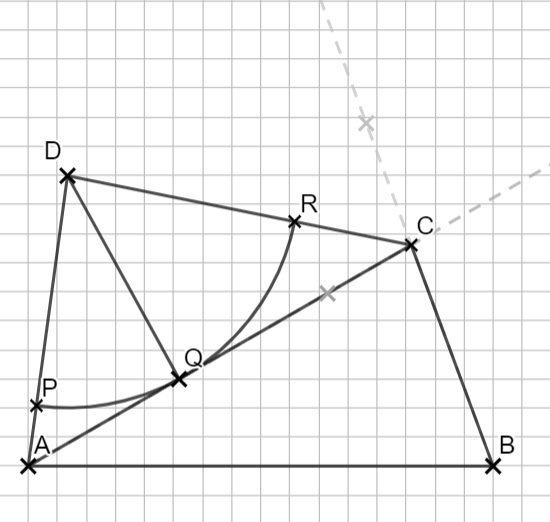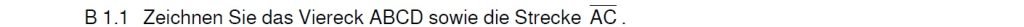
Lösung zu B1.1
Angabe für Angabe! Geodreieck und Zirkel bereithalten!
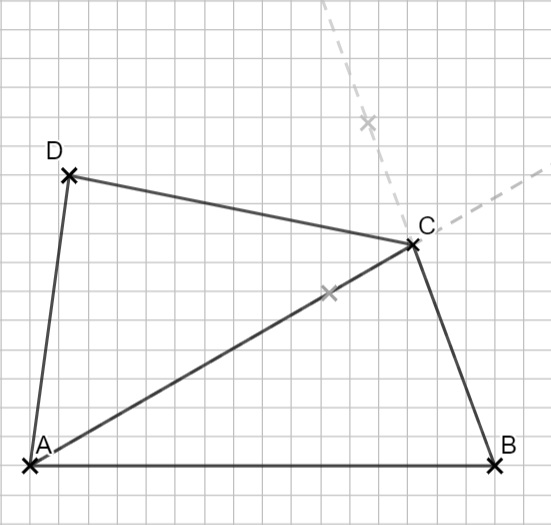
Zeichne zuerst \( \overline{AB} \). Zeichne dann beide Winkel ein. Du findest C im Schnittpunkt. Jetzt verwendest du deinen Zirkel um D zu finden.
Hier geht es zur allgemeinen Erklärung:
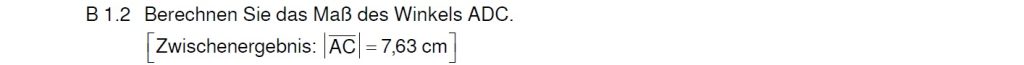
Lösung zu B1.2
Berechne immer zuerst das Zwischenergebnis, du wirst es brauchen!
Zerteilt man das Viereck entlang der Diagonalen AC, erkennst du bestimmt schnell:
Mit der Innenwinkelsumme im Dreieck ABC kannst du den Winkel bei C bestimmen unddann den Sinussatz verwenden. Anschließend kannst du den Cosinussatz im Dreieck ACD verwenden.
\begin{align} &|\overline{AC}| \text{ mit dem Sinussatz im Dreieck ABC}\\
\angle ACB &= 180° – 70° – 30° = 80°\\
\frac{|\overline{AC}|}{sin(\angle CBA)} &= \frac{|\overline{AB}|}{sin(\angle ACB)} \\
\frac{|\overline{AC}|}{sin(70°)} &= \frac{8}{sin(80°)}\,\,\, |\cdot sin(70°) \\
&\Rightarrow |\overline{AC}| = 7,63 cm \\
\\
&\angle ADC \text{ mit dem Cosinussatz im Dreieck ACD}\\
cos(\angle ADC) &= \frac{|\overline{AD}|^2 + |\overline{CD}|^2 – |\overline{AC}|^2}{2 \cdot |\overline{AD}| \cdot |\overline{CD}|}\\
cos(\angle ADC) &= \frac{5^2 + 6^2 – 7,63^2}{2\cdot 5\cdot 6} \,\,\, |cos^{-1} \\
&\Rightarrow \angle ADC = 87,34° \end{align}
Hier geht es zur allgemeinen Erklärung:

Lösung zu B1.3
Achtung, Winkelbezeichnung genau lesen. Es ist nicht so schwer!
Achte darauf, dass bei Q ein rechter Winkel ist! Das ist dann auch schon die Antwort auf die Frage: Es ist ein 90° Winkel.