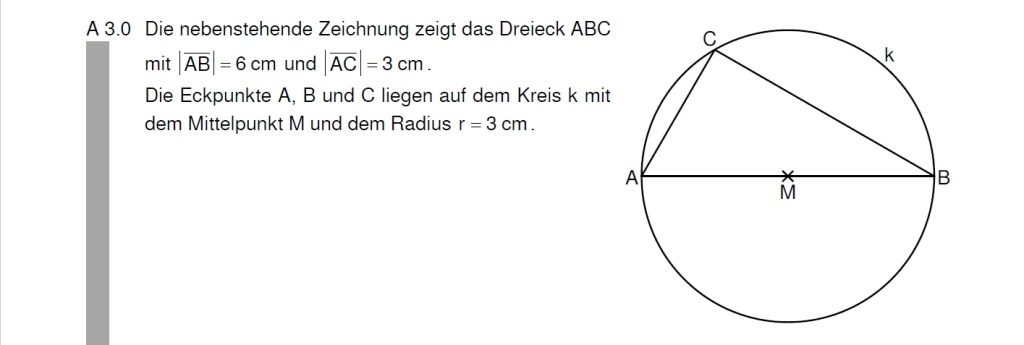
Lösung zu A3.1
90° nennen wir ja auch einen rechten Winkel … und da ist ein Kreis … da gab es doch so einen mathematischen Satz mit T.
Da \( |\overline{AB}| \) ein Durchmesser ist, liegt auf dem Thaleskreis und alle Winkel mit Scheitel auf der Kreislinie bilden einen 90° Winkel.
Gerade in der Produktion 🙂
Hier geht es zum wichtigen Grundwissen:
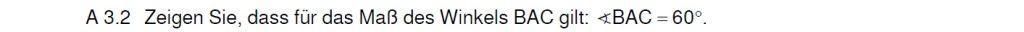
Lösung zu A3.2
Im rechtwinkligen Dreieck darfst du Sinus, Cosinus und Tangens verwenden. Für den Winkel brauchst du dann deine Formelsammlung.
Weil bei C ein rechter Winkel ist, kannst du mit Sin/Cos/Tan rechnen.
\begin{align} cos(\alpha) &= \frac{|\overline{AC}|}{|\overline{AB}|} \\
cos(\alpha) &= \frac{3}{6} = \frac{1}{2} \,\,\, |\text{in der Tabelle cos( ) = 0,5 nachschauen}\\
&\Rightarrow \alpha = 60° \end{align}
Gerade in der Produktion 🙂
Hier geht es zur allgemeinen Erklärung:
Lösung zu A3.3
Entweder verwendest du „Einhalb mal Grundseite mal Höhe“ oder die Sinusformel. Überleg‘ mal, was hier einfacher ist.
Setze in die Flächenformel mit dem Sinus ein und berechne mithilfe der Tabelle:
\begin{align} A &= 0,5 \cdot |\overline{AB}| \cdot |\overline{AC}|\cdot sin(60°) \\
&= 0,5 \cdot 6 \cdot 3 \cdot sin (60°) \\
&= 9 \cdot sin(60°) \,\,\, |\text{sin(60°) in der Formelsammlung in der Tabelle nachschauen:}\\
&= 9 \cdot \frac{\sqrt{3}}{2}\\
&\Rightarrow A = 4,5 \cdot \sqrt{3} \end{align}
Gerade in der Produktion 🙂