Lösung zu A2.1
An den Nenner erkennst du die Gesamtzahl der Lose. Am Zähler die Anzahl der Lose dieser Art.
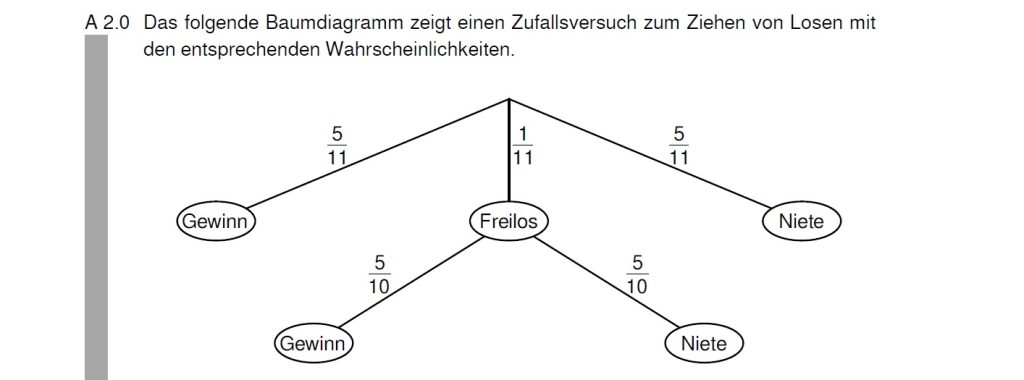
Die Nenner in der erster Zeile geben dir die Anzahl an Losen in der Urne. Die Zahl in den Nennern der Brüche ist 11, also gibt es 11 Lose. Auf den Bruchstrichen findest du die Anzahl dieser Loostypen.
Beim Freilos darf man nochmal ziehen, denn hier geht das Baumdiagramm weiter. Das alte Los wird nicht wieder reingelegt, denn das Freilos kann nicht nochmal gezogen werden. Dein Antwort könnte also lauten:
Aus einer Urne mit 11 Losen wird eines gezogen. Es gibt 5 Gewinne, 1 Freilos und 5 Nieten. Beim Freilos darf man nochmal ziehen.
Gerade in der Produktion 🙂
Hier geht es zur allgemeinen Erklärung:
Hier musst du ein Baumdiagramm „rückwärts zeichnen“. Das gab es bisher noch nie.
Lösung zu A2.2
Schaue ins Baumdiagramm! Welche Äste führen zu einem Gewinn? Ist es ein Ast, dann Pfadregel der Multiplikation. Sind es mehrere Äste? Dann Pfadregel der Addition.
Man gewinnt, wenn man entweder zuerst einen Gewinn zieht P(G) oder wenn man erst das Freilos und dann einen Gewinn zieht P(F|G). P(F|G) berechnest du mit der Pfadregel der Multiplikation. Die Endergebnisse werden mit der Pfadregel der Addition zusammengesetzt.
\begin{align} P(F|G) &= P(F) \cdot P(G) = \frac{1}{11} \cdot \frac{5}{10}= \frac{5}{110}\\
F(G) = \frac{5}{11} \\
\\
P_{ges} &= P(F|G) + P(G) \\
&= \frac{5}{110} + \frac{5}{11} \,\,\, |\text{Den zweiten Bruch mit 10 erweitern}\\
&= \frac{5}{110} + \frac{50}{110}\\
&\Rightarrow P_{ges} = \frac{55}{110} \end{align}
Gerade in der Produktion 🙂