
Lösung zu A2.1
Du hast den Scheitelpunkt gegeben. Es hat also etwas mit Scheitelform zu tun. Was könntest du mit einem Punkt, dem Scheitelpunkt und der Scheitelform machen, um an den Öffnungsfaktor zu kommen?
Setze den Scheitelpunkt für xs und ys ein und die Punkt P bei x und y. Wenn du dann vereinfachst, kommst du auf a.
\begin{align} y &= a \cdot (x – x_s)^2 + y_s &\text{ mit } S(2|3) \\
y &= a \cdot (x – 2)^2 + 3 &\text{ mit } P(0|1) \\
1 &= a \cdot (0 -2)^2 + 3 \\
1 &= a \cdot (-2)^2 + 3\\
1 &= a \cdot 4 + 3 \,\,\, |-3 \\
-2 &= a \cdot 4 \,\,\, |:4 \\
&\Rightarrow a =\, – 0,5 \end{align}
Lösung zu A2.2
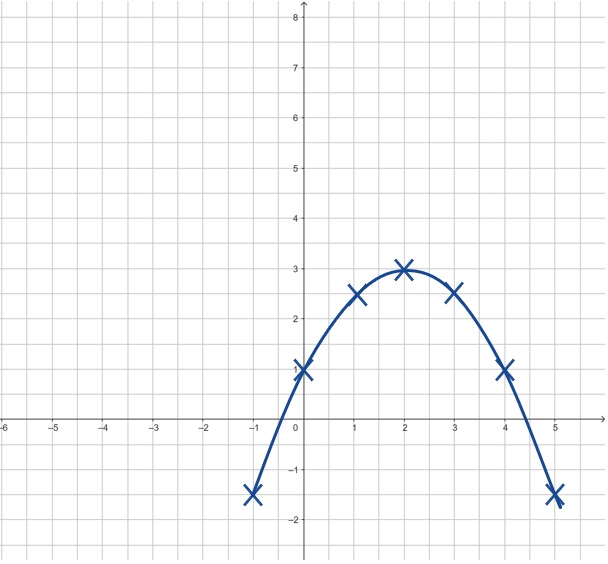
Zeichne den Scheitelpunkt ein und gehe quadratische Schritte. Aber nur die Hälfe und nach unten (a = -0,5)
Zeichne den Scheitel der Parabel ein und gehen von dort quadratische Schritte nach links und rechts. Aber wegen dem Öffnungsfaktor nur die Hälfte!
Wenn du das Vorgehen noch nicht kennst, schau am besten das Video!
Hier geht es zur allgemeinen Erklärung:

Lösung zu A2.3
Wenn du gerne nachdenkst, gehe nach dem Ausschlussprinzip vor.
Wenn du gerne rechnest, dann löse die Klammer in der Scheitelform mit der binomischen Formel aus und vereinfach, bis eine der vier Zeilen rauskommt.
Hier siehts du die Parabel in der allgemeinen Form \( y = ax^2 + bx + c \).
Der Öffnungsfaktor ist in dieser Aufgabe -0,5 , also kann es nur noch der zweite oder vierte Term sein. Überall steht in der Mitte 2x, hier kann man also nichts entscheiden.
Beim Vereinfachen müsste man die Klammer mit binomischer Formel ausmultiplieren und dann weiterrechnen.
Wenn ud kurz überlegst, musst du das aber nicht. Die binomische Formel hat hinten eine Zahl, die dann mit dem ys aus der Scheitelform verrechnet wird.
Die +3 in der Scheiteform bleiben nicht gleich. In der allgemeinen Form steht hinten nicht die gleiche Zahl, wie in der allgemeinen Form.
Daher kann es nicht der zweite Term sein, denn da steht hinten +3, genau wie in der Scheitelform.
Die richtige Antwort ist also der letzte Term.
Wenn dir das jetzt zu viel Text ist, dann nimm einfach die Scheitelform und vereinfache. Das geht auch.
