
Lösung zu A1.1
Markiere dir beide Äste im Baumdiagramm, die zur Aussage passen und berechne zuerst deren Wahrscheinlichkeiten.
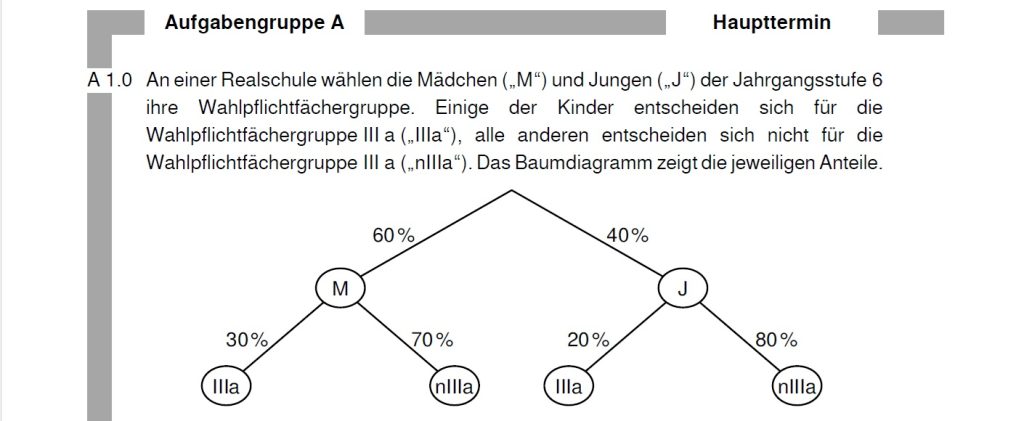
Die Wahrscheinlichkeit, dass das befragte Kind in IIIa ist, setzt sich aus zwei Ästen zusammen, nämlich aus Jungs in IIIa und Mädels in IIIa.
Du musst die Einzelwahrscheinlichkeiten der Äste durch Multiplikation bestimmen und dann addieren.
\begin{align}
P(M|IIIa) &= P(M) \cdot P(IIIa) \\
&= \frac{60}{100} \cdot \frac{30}{100} \\
&= \frac{6}{10} \cdot \frac{3}{10} = \frac{6\cdot 3}{10 \cdot 10} \\
& = \frac{18}{100}\\
\\
P(J|IIIa) &= P(J) \cdot P(IIIa) \\
&= \frac{40}{100} \cdot \frac{20}{100} \\
&= \frac{4}{10} \cdot \frac{2}{10} = \frac{4\cdot 2}{10 \cdot 10} \\
& = \frac{8}{100}\\
\\
P_{ges} &= \frac{18}{100} + \frac{8}{100} = 26 \% \end{align}
Hier geht es zur allgemeinen Erklärung:

Lösung zu A1.2
Es geht um die Prozentrechnung! 26% von allen Schülern sind gesucht.
Insgesamt sind es 150 Kinder und 26% gehen in die die WPFG IIIa. Kürze, bevor du rechnest, das macht es einfacher!
\begin{align} \frac{26}{100} \cdot 150 = \frac{26}{2}\cdot 3 = 13 \cdot 3 = 39. \end{align}
