

Lösung zu B4.1
Im geraden Prisma stehen die Kanten senkrecht auf die Grundfläche. Du darfst also Sin/Cos/Tan und den Satz des Pythagoras verwenden.
Zeichnung kommt mit dem Video
\begin{align} &|\overline{AN}| \text{ mit dem Satz des Pythagoras im Dreieck AMN:} \\
|\overline{AN}|^2 &= |\overline{AM}|^2 + |\overline{NM}|^2 \\
&= 5^2 + 8 ^2 \,\,\, |\sqrt{}\\
\Rightarrow &|\overline{AN}| = 9,43 cm \\
\\
&\angle CAN \text{ mit dem Tangens im Dreieck AMN:}\\
tan(\angle CAN) &= \frac{|\overline{NM}|}{|\overline{AM}|} \\
&= \frac{8}{5} \,\,\, |tan^{-1}\\
\Rightarrow &\angle CAN = 57,99° \end{align}
Hier geht es zur allgemeinen Erklärung:

Lösung zu B4.2
Selbst für eine Aufgabe zum Einzeichnen ist diese sehr lang! Langsam, aber sicher und Punkt für Punkt, dann klappt es schon.
Bild kommt mit dem Video.
Dann brauchen wir noch das erlaubte Intervall. Es entstehen Pyramiden, wenn die Spitze und die Grundfläche nicht in einer Ebene liegen. Oder anders gesagt: Wenn das P auf der Kante ganz nach oben gerutscht ist und auf N liegt, dann gibt es keine Pyramide, weil es keine Höhe mehr gibt. Das ist erreicht, wenn x = 9,43 ist. Ein Wert von x = 0 ist erlaubt, dann liegen die neuen Punkte eben auf A,B,C und D. Das ist aber kein Problem. In mathematischer Schreibweise:
\( 0 \leq x < 9,43 \)
Hier geht es zur allgemeinen Erklärung:

Lösung zu B4.3
Schreibe dir die Formel für den Flächeninhalt des Drachenvierecks auf und versuche die einzelnen Strecken zu bestimmen. Für eine brauchst du den Vierstreckensatz.
Schreibe dir immer einmal die Flächenformel auf, denn darann kannst du dir überlegen, welche Strecken zu berechnen musst.
\begin{align} A &= \frac{1}{2} \cdot e \cdot f \\
&= \frac{1}{2} \cdot |\overline{Q_n S_n}| \cdot |\overline{P_n R_n}| \end{align}
Die erste Diagonale ist nicht schwer, sie hat die gleiche Länge wie die Diagonale unter ihr.
\( |\overline{Q_n S_n}| = |\overline{BD}| = 10 \)Die zweite Diagonale braucht mehr Aufmerksamkeit. Sie setzt sich aus der unbekannten Strecke a auf der linken Seite und 5 cm auf der rechten Seite zusammen. Auf der linken Seite kann man den 4-Streckensatz verwenden, um a auszurechnen.
\begin{align} \frac{a}{|\overline{AM}|}&= \frac{|\overline{NP_n}|}{|\overline{AN}|} \\
\frac{a}{5} &= \frac{9,43 \, – \,x}{9,43} \\
\frac{a}{5} &= \frac{9,43}{9,43} \,- \, \frac{x}{9,43} \\
\frac{a}{5} &= 1 \, – \, \frac{x}{9,43} \,\,\, |\cdot 5\\
a &= (1 \, -\, \frac{x}{9,43}) \cdot 5 \\
\Rightarrow &a = 5 – 0,53x \\
\Rightarrow &|\overline{P_n R_n}| = 5 \, – \, 0,53x + 5 = 10 \, – \, 0,53x \\
\\
A &= \frac{1}{2} \cdot 10 \cdot (10 – 0,53x) \\
&= 5 \cdot (10 \, – \,0,53x) \\
\Rightarrow &A = (50 \, – \, 2,65x) cm^2 \end{align}
Hier geht es zur allgemeinen Erklärung:
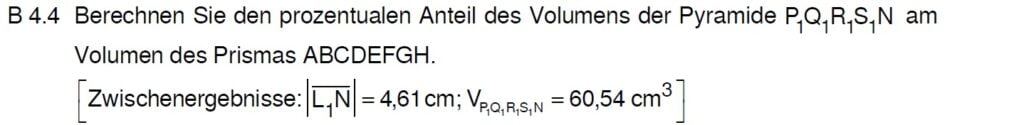
Lösung zu B4.4
Berechne die neue Höhe der Pyramide, indem du von der Höhe des Prisma das „Zu viel“ abziehst. Berechne dann die Grundfläche mit der Formel aus 4.3 für x = 4. Den Rest bekommst du dann alleine hin.
Zuerst berechnest du die Höhe der Pyramide. Dazu ziehst du von der Höhe des Prismas den Teil ab, der zuviel ist. Ich habe diesen Teil einfach mal b genannt. Diesen musst du natürlich erst ausrechnen.

\begin{align}
sin(\angle CAN) &= \frac{b}{|\overline{AP_1}|} \\
sin(57,99°) &= \frac{b}{4} \,\,\, |\cdot 4 \\
\Rightarrow &b = 3,39\\
&\Rightarrow |\overline{L_1 N}| = h = 8 \, – \, 3,39 = 4,61 cm \end{align}
Um das Volumen der Pyramide zu bestimmen, brauchen wir jetzt noch die Grundfläche. Hier machst du dir natürlich das Leben einfach und berechnest diese mit der Formel aus 4.3, indem du sie für x = 4 ausrechnest.
\begin{align} A(x) &= 50 – 2,65 x \\
A(4) &= 50 – 2,65 \cdot 4 = 39,4 cm^2 \end{align}
Jetzt kannst du alles einsetzen.
\begin{align} V &= \frac{1}{3} \cdot A(4) \cdot h \\
&= \frac{1}{3} \cdot 39,4 \cdot 4,61 \\
\Rightarrow &V = 60,54 cm^3 \end{align}
Eigentlich wäre das genug, um zur nächsten Teilaufgabe zu gehen, aber diese Aufgabe ist wirklich lange! Als nächstes brauchst du das Volumen des Prismas, um den Anteil aufzustellen. Danach kommt nur noch Prozentrechnung.
\begin{align} V_{Prisma} &= A_g \cdot h \\
&= \frac{1}{2} \cdot e \cdot f \cdot h \\
&= \frac{1}{2} \cdot 10 \cdot 10 \cdot 8 \\
&\Rightarrow V_{Prisma} = 400 cm^3 \\
\\
p &= \frac{V}{V_{Prisma}} = \frac{60,54}{400} = 0,1514 = 15,14 \% \end{align}
So, das war es dann wirklich. Was für eine „tolle“ Aufgabe.
Hier geht es zur allgemeinen Erklärung:

Lösung zu B4.5
Zeichne in einer Skizze verschiedene Winkel ein und überlege, wann der Winkel größer wird. Vielleicht musst du den Winkel ja garnicht ausrechnen, sondern du kennst ihn schon.
Der größte Winkel entsteht, wenn R und P weit unten sind. Am weitesten unten sind sie für x = 0. In diesem Fall liegt P auf A und R auf C. Der Winkel NRP ist auf der rechten Seite, aber aufgrund von Symmetrie genauso groß wie CAN. Es gilt also:
\( \angle NR_0 P_0 = \angle CAN = 57,99° \)