2024 Nachtermin B3: Ebene Geometrie

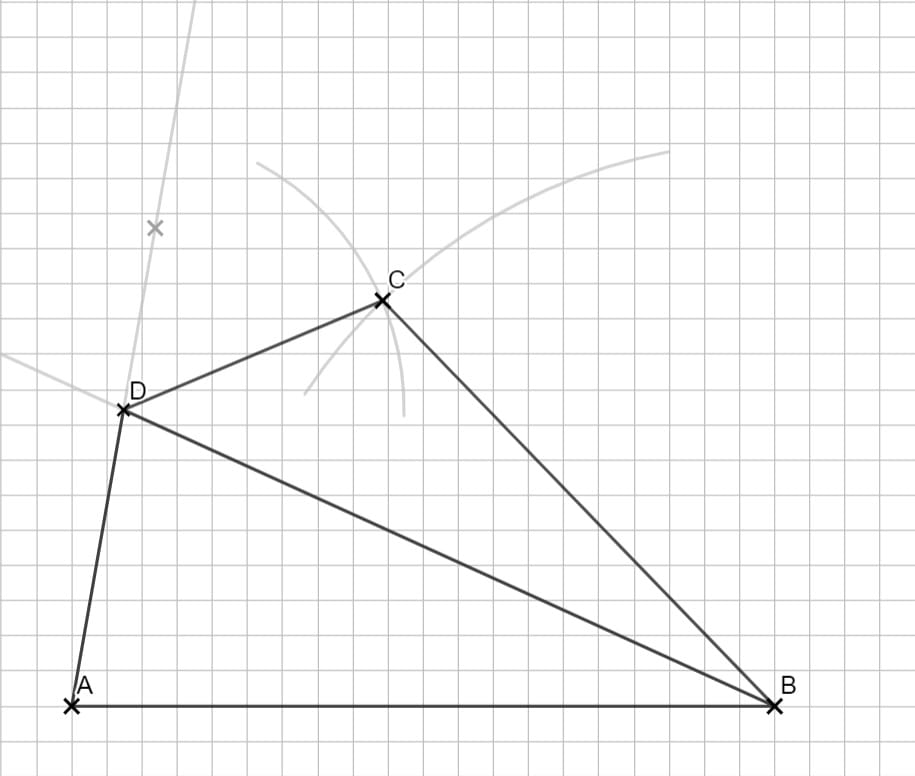
Im Dreieck BCD hast du nur 2 Angaben, also kannst du darin nicht rechnen. Im Dreieck ABD hast du 3 Angaben, allerdings passen sie nicht zu unseren Ansätzen. Um den Sinussatz verwenden zu können, brauchst du den Winkel bei D, weil du die gegenüberliegende Streckenlänge kennst. Also zuerst Innenwinkelsumme im Dreieck ausnutzen, dann mit Sinussatz rechnen.

\begin{align} &\angle ADB \text{ mit der Innenwinkelsumme in ABD:}\\
\angle ADB &= 180° – \angle BAD – \angle DBA = 180° – 80° – 25° = 75° \\
\\
&|\overline{BD}| \text{ mit dem Sinussatz im Dreieck ABD}\\
\frac{|\overline{BD}|}{sin(\angle BAD)} &= \frac{|\overline{AB}|}{sin(\angle ADB)} \\
\frac{|\overline{BD}|}{sin(80°)} &= \frac{10}{sin(75°)} \,\,\, |\cdot sin(80°) \\
\Rightarrow & |\overline{BD}| = \frac{10}{sin(75°)} \cdot sin(80°) = 10,20 cm \end{align}

Zeichnung kommt mit dem Video

Weil bei F ein rechter Winkel ist, kennen wir im Dreieck BEF drei Dinge: Winkel bei B (25°), Winkel bei F (90°) und den Abstand von B zu E (4cm). Weil die 4cm gegenüber des rechten Winkels sind, ist das die Hypotenuse und du sollst die Ankathete des Winkels ausrechnen. Der passende Ansatz ist also …

\begin{align} &|\overline{BF}| \text{ mit dem Cosinus im Dreieck BEF:}\\
cos(\angle DBA) &= \frac{|\overline{BF}|}{|\overline{BE}|} \\
cos(25°) &= \frac{|\overline{BF}|}{4} \,\,\, |\cdot 4 \\
\Rightarrow &|\overline{BF}| = cos(25°) \cdot 4 = 3,63 cm \end{align}

An parallelen Geraden entstehen Stufenwinkel. Sie sind jeweils „auf der selben Seite“ der Schnittpunkte. Der Wikel DBA und der Winkel GFA sind beide „oben links“. Also sind sie Stufenwinkel und gleich groß. Achtung, das funktioniert nur an parallelen Geraden. In mathematischer Schreibweise:

\( GF || BD \, \Leftrightarrow \, \angle GFA = \angle DBA \) (Stufenwinkel)

Parallele Geraden sind auch immer einen Hinweis auf den Vierstreckensatz. Dieser auch ein richtiger Ansatz!
Du kannst aber auch im Dreieck AFG die Länge von \(\overline{AF}\) und das Maß des Winkels bei G berechnen, um dann den Sinussatz zu verwenden. Das braucht zwar ein paar Zwischenschritte, geht aber auch.

\begin{align} |\overline{AF}|&= |\overline{AB}| – |\overline{FB}| = 10 – 3,63 = 6,37 cm \\
\angle AGF &= 180° – 80° – 25° = 75° \\
\\
&|\overline{FG}| \text{ mit dem Sinussatz im Dreieck AFG:}\\
\frac{|\overline{FG}|}{sin(\angle FAG)} &= \frac{|\overline{AF}|}{sin(\angle AGF)} \\
\frac{|\overline{FG}|}{sin(80°)} &= \frac{6,37}{sin(75°)} \,\,\, |\cdot sin(80°) \\
\Rightarrow & |\overline{FG}| = \frac{6,37}{sin(75°)} \cdot sin(80°) = 6,49 cm \end{align}

Im Dreieck BCD hast du inzwischen 3 Angaben und kann den Winkel mit dem Cosinussatz berechnen.

\begin{align} cos(\angle DCB) &= \frac{|\overline{BC}|^2 + |\overline{DC}|^2 – |\overline{DB}|^2}{2\cdot |\overline{DC}| \cdot |\overline{BC}|}\\
&= \frac{8^2 +4 ^2 – 10,20^2}{2\cdot 8 \cdot 4} \,\,\, |cos^{-1}\\
\Rightarrow &\angle DCB = 112,06° \end{align}

Zerteile das Viereck entlang BD und berechne den Flächeninhalt der Dreiecke mit der Sinusformel.

\begin{align}A_{ABD} &= \frac{1}{2} \cdot |\overline{BD}| \cdot |\overline{AB}| \cdot sin(\angle DBA) \\
&= \frac{1}{2} \cdot 10 \cdot 10,20 \cdot sin(25°) \\
\Rightarrow &A_{ABD} = 21,55 cm^2 \\
A_{BCD} &= \frac{1}{2} \cdot |\overline{CD}| \cdot |\overline{BC}| \cdot sin(\angle DCB) \\
&= \frac{1}{2} \cdot 4 \cdot 8 \cdot sin(112,06°) \\
\Rightarrow &A_{BCD} = 14,83 cm^2 \\
\\
\Rightarrow &A_{ABCD} = 21,55 + 14,83 = 36,38 cm^2 \end{align}

Aus 3.4 kennst du den Flächeninhalt des Vierecks. Daraus kannst du den Flächeninhalt des Kreissektors berechnen. Achtung: 33% sind streng genommen 0,33 und nicht 1/3.

\begin{align} A_{Kreissektor} &= 33 \% \cdot 36,38 = 12,01 cm^2 \end{align}

Jetzt die Formel für den Flächeninhalt nehmen, alles einsetzen und nach r auflösen.

\begin{align}
A &= \frac{\alpha}{360°} \cdot r^2 \cdot \pi \\
12,01 &= \frac{112,06°}{360°} \cdot r^2 \cdot \pi \,\,\, |:\pi \\
\frac{12,01}{\pi} &= \frac{112,06°}{360°} \cdot r^2 \,\,\, |:\frac{112,06°}{360°}\\
\frac{12,01}{\pi} :\frac{112,06°}{360°} &= r^2 \,\,\, |\sqrt{}\\
\Rightarrow &r = \sqrt{\frac{12,01}{\pi} :\frac{112,06°}{360°}} = 3,50 cm \end{align}