
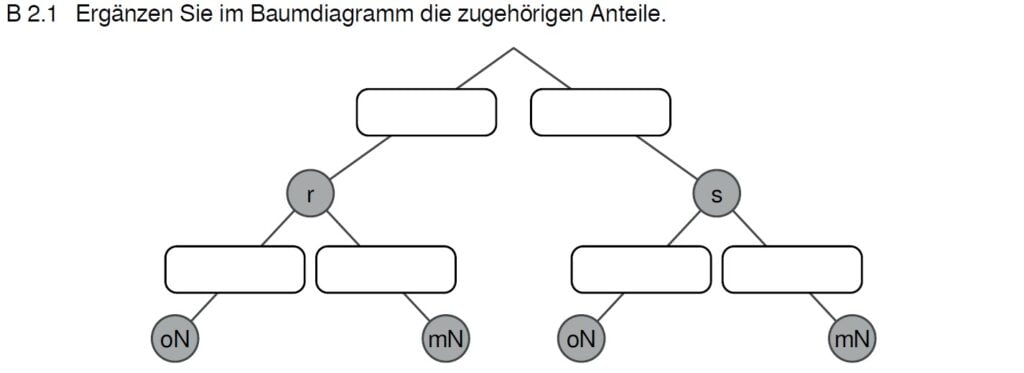
Lösung zu B2.1
Die Gegenwahrscheinlichkeit ergibt sich immer zu 100%. 24% auf der einen Seite, also 76% auf der anderen.
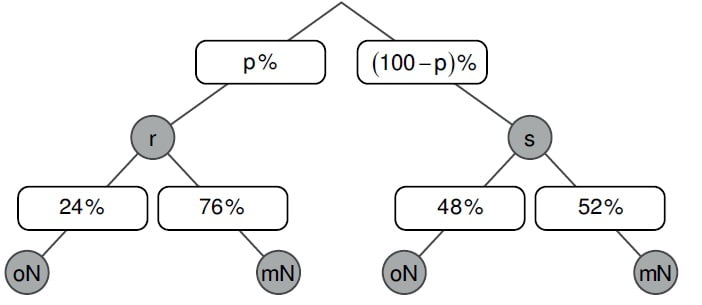
Hier geht es zur allgemeinen Erklärung:

Lösung zu B2.2
Die Wahrscheinlichkeit entlang des Astes ist 18%. Stelle mit der Pfadregel der Multiplikation eine Gleichung auf.
\begin{align} P(r| oN) &= P(r) \cdot P(oN) \\
\frac{18}{100} &= \frac{p}{100} \cdot \frac{24}{100} \,\,\, |:\frac{24}{100} \\
\frac{18}{100} : \frac{24}{100} &= \frac{p}{100}\,\,\, \text{mit dem Kehrbruch multiplizieren:}\\
\frac{18}{100} \cdot \frac{100}{24} &= \frac{p}{100}\\
\frac{18}{24} &= \frac{p}{100} \,\,\, |\cdot 100\\
&p = \frac{18}{24} \cdot 100 = 75 \end{align}
Hier geht es zur allgemeinen Erklärung:

Lösung zu B2.3
Zwei Äste passen zur Aussage. Berechne diese einzeln und setze dann zum Gesamtergebnis zusammen.
\begin{align} P_{ges} &= P(r| mN) + P(s| mN) \\
\\
P(r | mN) &= P(r) \cdot P(mN) \\
&= \frac{75}{100} \cdot \frac{76}{100} \\
&= \frac{57}{100}\\
\\
P(s |mN) &= P(s) \cdot P(mN)\\
&= \frac{25}{100}\cdot \frac{52}{100}\\
&= \frac{13}{100} \\
\\
P_{ges} &= \frac{57}{100} + \frac{13}{100} = \frac{70}{100} \end{align}
